Н.А. Мытник
КРАТКАЯ ИСТОРИЯ КОРАБЕЛЬНЫХ НАУК
(хронология событий с комментариями)
Глава 3. Период становления и революционного развития корабельной науки
( с 1855 по 1906 год)
(Продолжение)
В середине XIX века своеобразной революцией в гидромеханике явился переход от абстрактного безвихревого или потенциального движения жидкости к более реальному вихревому. В 40-50-х годах сначала французский математик Огюстен Коши (1789-1857 гг.), а затем и в 1856 г. немецкий математик и физик Герман Гельмгольц (1821-1894 гг.) при аналитическом и физическом исследовании вихрей в сплошной среде разрабатывают основы вихревой теории жидкости, в соответствии с которой скорость v в любой точке завихренной жидкости может быть разложена на следующие составляющие
v = v0 + v1 + v2 , (1856 г.)
где v0 - вектор скорости поступательного движения произвольной точки частицы жидкости, выбранной в качестве полюса; v1 - вектор скорости деформационного движения; v2 = w
d r - вектор скорости вращательного движения частицы вокруг полюса с мгновенной угловой скоростью w;
d r = i d x + jd
y + kd z - элементарный вектор, характеризующий положение рассматриваемой точки относительно полюса.
При этом Гельмгольцем было введено понятие вихря скорости rot v = 2
w .
 |
Краткая биографическая справка:
Огюстен Коши, французский математик, член Парижской академии наук. Окончил Политехническую школу и Школу мостов и дорог в Париже, работал инженером в Шербуре, преподавал в Политехнической школе и Коллеж де Франс. Основоположник теории аналитических функций комплексного переменного, автор трудов по теории дифференциальных уравнений, математической физике, теории чисел и вычетов, геометрии, классических курсов по математическому анализу, работ по алгебре, теории упругости, гидромеханике и оптике. |
 |
Краткая биографическая справка:
Герман Гельмгольц, немецкий физик, гидромеханик, математик, физиолог и психолог, профессор, член-корреспондент Петербургской академии наук. Окончил Военно-медицинский институт в Берлине, преподавал в берлинском Физико-техническом институте. Впервые дал математическое обоснование закона сохранения энергии, распространил принцип механического подобия на природные явления. Автор термодинамической теории химических процессов и аномальной дисперсии. Труды по вихревой теории, аэродинамике и воздухоплаванию, физиологии слуха и зрения, биофизике. |
События 1856 г.
- На озере Мьеса в Норвегии начались рейсы колесного парохода “Скибландер”, который за 129 последующих лет эксплуатации прошел всего два капитальных ремонта (!).
- В Англии заложен самый большой за всю историю деревянный парусно-винтовой боевой корабль - 131-пушечный линейный корабль “Мальборо” (D=6100 т, L=74,7 м).
- Трансатлантический лайнер “Персия”(BRT=3300 рег.т) - первый кунардовский железный пароход, - выдерживает сильное лобовое столкновение с айсбергом благодаря своему металлическому корпусу. После ремонта через год он вновь завоевывает Голубую ленту, впервые преодолев дистанцию менее чем за 10 суток.
- Английский механик Рутвен вместе с кораблестроителем Сейделем устанавливает роторный водометный движитель на небольшом паровом судне “Алерт”, который им был испытан на небольшой шлюпке еще в 1839 г.
- Американский изобретатель Филипс создает жесткий скафандр с клещами-захватами, защищающий от давления все конечности водолаза и перемещаемый в воде гребным винтом с ручным приводом.
- В Петербурге на Васильевском острове основан Балтийский завод - крупнейшее судостроительное предприятие России.
- Испытания в России подводной лодки немецкого артиллериста Бауэра, признанной несовершенной и бесполезной.
- Безуспешные поиски трансатлантического лайнера Э.Коллинза “Пасифик”(BRT=2860 рег.т), пропавшего без вести вместе с 200 пассажирами в Сев.Атлантике вероятнее всего в результате столкновения с айсбергом.
- Английский капитан Вильям Скорсби (1789-1857 г.) на корабле “Ройал Чартер” отправляется в последнее плавание к берегам Австралии для изучения магнитной девиации, на основании исследований которого Ливерпульский комитет устанавливает зависимость наиболее сильной полукруговой девиации от постоянного и возбужденного магнетизма корабля.
- Гибель во время шторма в Балтийском море русского 84-пушечного линейного корабля “Лефорт” от потери остойчивости, в результате чего погибли 827 человек, в том числе 53 женщины и 17 детей.
- Передана в дар Японии шхуна “Хеда” (D=106 т, L=21,3 м), построенная экипажем фрегата “Диана”, прибывшего с дипломатической миссией Ефима Путятина (1804-1883 гг.) в Японию и погибшего там в результате землетрясения. Принимая участие в постройке этой шхуны, японцы после ее отплытия в Петропавловск заложили по чертежам “Хеды” сразу три таких же корабля, впервые освоив, таким образом, европейскую технологию судостроения.
В 1860 г. английский ученый Файбери предложил обеспечивать общую продольную прочность кораблей условной постановкой его корпуса на скалу при обеспечении равновесия носовой и кормовой частей, что позволило внести единообразие в определении расчетного изгибающего момента на корпусе.
В этом же году Бурачек, посвятивший многие годы проектированию и совершенствованию
водометных движителей, опубликовывает научную работу, в которой даются основы теории и различные конструкции этого типа движителя. Однако реализовывать предложения Бурачека так никто и не стал, в том числе проект водометного движителя под строящийся в США крейсер “Генерал-Адмирал”.
Говоря о научной деятельности Бурачека, которая к сожалению не получила в свое время мирового признания, необходимо отметить, что к этому времени он впервые в отечественной практике разрабатывает также и теорию сопротивления воды движущимся телам и кораблю в частности, основанную на идее использования модельных испытаний, в каких-то моментах опередив на 10 лет общеизвестную методику Фруда. Более того, на основании этой теории он создает и оригинальный метод вычисления потребной мощности главных судовых двигателей.
Примечательно также то, что по предложению Бурачека науку о корабле с методической точки зрения стали делить на три взаимосвязанных, но самостоятельных дисциплины: теорию корабля, корабельную архитектуру (проектирование) и науку о прочности корпуса. Эти три базовых компонента корабельная наука содержит до сих пор.
События 1860 г.
- Год на французском флоте несет боевую службу первый мореходный броненосец - деревянный паровой винтовой корабль “Ля Глоар”, построенный по проекту Дюпюи де Лома и вооруженный пушками, заряжающимися, в отличие от английских, с казенной части.
- В Англии спущен на воду первый в мире железный винтовой броненосец “Уорриор”, который до сих пор сохранился в качестве плавучего музея в Портсмуте.
- Итальянский электротехник Антонио Пачинотти (1841-1912 гг.) создает электродвигатель с вращающимся кольцевым якорем, нашедший впоследствии повсеместное применение в качестве главного двигателя на подводных лодках и привода многих судовых механизмов.
- Французский изобретатель Этьен Ленуар (1822-1900 гг.) создает первый в мире двигатель внутреннего сгорания, работающий на светильном газе без предварительного сжатия горючей смеси.
- Английский кораблестроитель Купер Кольз (1819-1870 гг.) патентует орудийную башню.
- Французский электротехник Планте создает первый свинцово-кислотный аккумулятор, нашедший быстрое применение на подводных лодках.
- Экспедиция англо-американской эскадры в Никарагуа для захвата последнего из флибустьеров - Вильяма Уокера.
С 1861 по 1875 г. английский ученый Вильям Фруд (1810-1879 гг.) разрабатывает
линейную гидродинамическую теорию бортовой качки судна на регулярном волнении (для идеальной жидкости), которая впервые была опубликована в 1865 г.
и была основана на гипотезе о малости размеров судна по сравнению с размерами волн. Таким образом, на смену упрощенной теории бортовой качки Д.Бернулли приходит более совершенная теория, которая впоследствии будет учеными неоднократно совершенствоваться, пока не примет современный вид как основной инструмент кораблестроителей в исследовании качки судов.
Краткая биографическая справка:
Вильям Фруд, английский корабельный инженер и ученый. Окончил колледж в Оксфорде, член Английского королевского общества. Участвовал в постройке “Грейт Истерна”, по предложению Брунеля занялся изучением качки и сопротивления движению судна, автор трудов в области теории корабля, теоретической и экспериментальной гидродинамики, создатель первого в мире современного опытового бассейна. Разработал методику проведения модельных и натурных испытаний судов, изобретатель фрикционного маятника.
|
 |
Суть линейного подхода в задачах гидродинамики состоит в использовании при решении уравнения Лапласа граничных условий только с линейными членами, предполагая скорости перемещения судна и жидкости в каждый момент времени пренебрежимо малыми. С учетом малости также и амплитуд колебаний судна и жидкости это в итоге приводит к тому, что характеристики качки судна - перемещения, скорости и ускорения, - оказываются линейно связанными с соответствующими характеристиками волнения.
Система линеаризованных граничных условий для судна без хода по поверхности воды
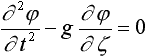 ;
;
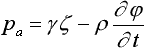 (уравнение Лагранжа); (1865 г.)
(уравнение Лагранжа); (1865 г.)
по корпусу судна 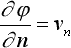 ,
,
где j - потенциал скорости абсолютного движения жидкости, м2/с; t - время, с; g - ускорение свободного падения, м/с2; z - ордината точки в жидкости, м; pа - атмосферное давление, н/м2;
g - удельный вес воды, н/м3;
r - плотность воды, кг/м3; n -
нормаль к смоченной поверхности судна; vn - нормальная составляющая скорости тела (смоченной поверхности корпуса), м/с.
Интересно отметить, что теория бортовой качки Д.Бернулли во времена парусного судостроения использовалась кораблестроителями не так часто. Это объяснялось не столько невысокой ее точностью, сколько тем, что парусники имели в целом слабую качку из-за демпфирующего действия парусов и рангоута, и чем была выше скорость ветра, тем качка становилась незаметнее. Правда, при этом, судну приходилось двигаться, как правило, под каким-то постоянным углом крена.
Ко времени завершения создания Фрудом новой теории бортовой качки практическая потребность в ней коренным образом изменилась. В это время боевые корабли начали интенсивно избавляться от своего парусного вооружения, что сразу обострило и проблему их качки. Еще во времена Д.Бернулли была известна связь параметров качки и остойчивости, однако теперь учет характеристик волнения позволял более точно прогнозировать поведение корабля в море.
Как и всякий колебательный процесс качка не только дурно влияет на механизмы и грузы, но, в первую очередь, - и на человека: морская болезнь при резкой и порывистой качке делает затруднительным не только выполнение экипажем элементарных боевых операций, но и способна полностью вывести корабль из строя, даже эффективнее, чем это сделает противник другими средствами.
В том же 1865 г. английский ученый Вильям Рэнкин (1820-1872 гг.), который явился основоположником технической термодинамики, разрабатывает дисковую теорию движителя (теорию идеального движителя), усовершенствованную затем в 1883 г. Фрудом и в 1910 г. русскими инженерами Г. Сабининым и Б. Юрьевым. Эта теория идеального движителя на долгое время станет единственной работоспособной для кораблестроителей со времен Традголда (рис.34).

vo + wa vo + wa/2 vo
Рис.34. Схема дисковой теории винта: 1 - диск винта площадью SД; 2 - эпюра гидростатического давления.
Р = m wa ,
где Р - упор движителя, н; m = r SД
vc - масса воды, проходящая через диск винта в единицу времени,
кг/c; wa - аксиальная скорость потока, вызванная движителем, м/c;
r - плотность воды, кг/м3; SД
- площадь диска движителя, м2; vс = v0 + wa/2 - скорость в диске движителя, м/c; v0 - cкорость набегающего на движитель потока воды или скорость судна, м/с.
В 1865 г. издается и фундаментальный труд Окунева “Теория и практика судостроения”,
в котором, в частности, впервые представлено уравнение весов в более общем виде, учитывающее наличие на судне машинной установки и запасов топлива для нее. Эта работа Окунева явилась значительным вкладом в теорию проектирования новых для того времени паровых судов и намного опередила свое время, так как позволила связать требования к ходкости с искомым водоизмещением судна.
Можно сказать, что научные работы Окунева, получившие мировое признание, официально открыли “русский” вклад в развитие корабельных наук.
События 1865 г.
- В Англии спущен на воду первый казематный броненосец “Беллерофон”, спроектированный главным кораблестроителем Э. Ридом.
- Успешная эксплуатация переоборудованного буксирного парохода кронштадтского купца Михаила Бритнева (1822-1889 гг.) “Пайлот” по продлению навигации между Кронштадтом и Ориенбаумом, на котором форштевень был срезан под углом 20 о.
- Начало перевода во многих развитых странах котельных установок на жидкое топливо.
- Русский инженер и изобретатель Иван Александровский (1817-1894 гг.) разрабатывает проект первой самодвижущейся мины, которые в начале 20 века стали называть торпедами.
- Начальником Кронштадтской компасной обсерватории назначен Иван Белавенец (1829-1878 гг.) - русский ученый-девиатор, первый размагничивший в 1863 г. корабль - броненосную батарею “Первенец”.
- Удачные испытания на переоборудованном деревянном линейном корабле “Ройал Соверин” орудийных башен К.Кольза, которые им были разработаны после применения в 1862 г. Дж.Эриксоном на броненосце “Монитор” первых орудийных башен.
- Год эксплуатации английских гражданских судов с корпусами из мартеновской стали - винтового парохода “Энни” и двух парусников: “Формбай” и “Альтеа”, на которых корпуса оказались легче на 20 -25% по сравнению с железными.
- В Гельсингфорсе основана финская судостроительная компания “Вяртсиля”.
В 1866 г. Рэнкин вносит свой вклад и в общую прочность корабля - предлагает разделять общий изгибающий момент, действующий на корпус, на две составляющие: волновую (на волне трохоидального профиля) и на тихой воде. Этот подход в оценке общей продольной прочности корабля используется кораблестроителями и до настоящего времени.
События 1866 г
- Обладателем Голубой ленты Атлантики становится впервые лайнер английской компании Инман лайн - двухвинтовой пароход “Сити оф Пэрис”(BRT=2651 рег.т, v=13,5 уз).
- После выхода из строя первого подводного кабеля брунелевским пароходом “Грейт Истерн” проложен третий и восстановлен второй трансатлантические подводные телеграфные кабели.
- В России построена первая в мире подводная лодка с единым пневматическим двигателем (D=363 т) по проекту И. Александровского, разработанному в 1862 г.
- Знаменитая гонка 16 чайных клиперов, среди которых в упорной борьбе английские клиперы кораблестроителя Роберта Стила “Ариэль” и “Тайпин” пришли из Китая в Англию за 99 суток с разницей в 10 минут (!).
- Английский заводчик Уайтхэд на своем заводе в Фиуме (Австрия) изготавливает первую запатентованную торпеду, которая в начале 70-х годов стала выпускаться серийно.
- В США строится казематный деревянный броненосец “Данденбург” (D=7100 т), оказавшийся в истории судостроения самым длинным деревянным боевым кораблем (L=115 м).
- Сравнительные испытания одинаковых по водоизмещению английских пароходов - винтового “Волонтер” и водометного “Наутилус” с движителем Рутвена, показавшие преимущества водометного движителя. Однако через год соревнование канонерских лодок - водометной “Уотер Уич” и винтовой “Вайпер” (D=1280 т) с более совершенным винтом оказалось не в пользу водометных движителей.
- Английские электротехники Кромвель и Варли создают первый электрогенератор.
- В США построена первая подводная лодка с мускульным приводом “Интеллижент уэйл”, имеющая специальное устройство, позволяющее покидать лодку и возвращаться в нее.
- Первое сражение паровых деревянных броненосцев у о. Лисса в Адриатическом море между австрийской (В. Тегетгоф, 21 кор) и итальянской (К. Персано, 19 кор) эскадрами, закончившееся потоплением флагманского итальянского броненосца “Ре ДI Италия”, протараненного австрийским броненосцем “Фердинанд Макс”, и пожаром с последующим взрывом на другом итальянском броненосце.
- В гроте о. Разочарований в Новой Зеландии разбивается английский парусник “Генерал Грант”, золото которого до сих пор не дает покоя морским золотоискателям.
- В Тихом океане между Гавайскими островами и Мексикой сгорел американский клипер “Хорнет”, в результате чего из трех шлюпок удалось дойти до Гавайских островов, преодолев 4000 миль, только одной. Трагедию этой катастрофы впервые описал, будучи журналистом, Марк Твен.
В 1869 г., когда Рассел опубликовал свою теорию сопротивления воды, которая для кораблестроителей давала не много практических рекомендаций, Вильям Фруд формулирует закон гидродинамического подобия, который до настоящего времени является одним из главных инструментов при проектировании судов: “Сопротивления формы двух геометрически подобных судов соотносятся между собой как кубы линейных измерений, в то время как их скорости будут находиться в отношении корня квадратного из их измерений”
[5].
Открытие этого закона было вызвано крайней необходимостью определения в процессе проектирования судна достоверного значения мощности, требующейся для движения корабля с заданной скоростью в зависимости от его размеров и формы. К тому времени кораблестроителям при создании мощных броненосцев и крейсеров все чаще и чаще приходилось расплачиваться за ошибки в определении мощности энергетической установки ценой невыполнения контрактных скоростей хода. Этим, отчасти, объяснялось и то, что кораблестроители тогда не торопились избавить свои корабли от парусного вооружения, подстраховывавшего их от подобных неприятностей.
В соответствии с открытым законом второй после числа Эйлера критерий гидродинамического подобия - число Фруда будет представлять из себя отношение сил инерции к силам веса.
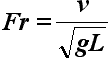 ;
;
 ; (1869 г.)
; (1869 г.)
RH = RM (LH/LM)3,
где Fr - число Фруда; g - ускорение свободного падения, м/с2; L - длина судна, м; v - скорость судна, м/c; R - сопротивление судна, н; М - индекс модели; Н - индекс натурного судна.
Для проверки своей методики Фруд впервые проводит буксировку натурного парового судна - корвета “Грейхаунд”.
События 1869 г.
- В Египте завершилось строительство Суэцкого канала, осуществляемое по проектам инженеров Линана, Мужеля и Негрелли в течение 10 лет.
- В Глазго построен клипер “Катти Сарк”, который является единственным судном этого типа, сохранившимся до наших дней (с 1957 г. - плавучий музей в Гринвиче).
- Установление английским чайным клипером “Сэр Ланселот” на маршруте Китай - Англия абсолютного рекорда продолжительности плавания для кораблей своего типа - 90 суток.
- В Англии проходит испытания первый железный винтовой крейсер “Инкостант” (D=5800 т, v=16,5 уз) с полным парусным вооружением.
Научные исследования английского физика и математика Джорджа Стокса
(1819-1903 гг.) в 60-х годах XIX века позволили значительно развить вихревую теорию жидкости - им была выведена теорема, позволяющая связать циркуляцию и вихрь скорости: циркуляция скорости по замкнутому контуру, ограничивающему односвязную область жидкости, равна потоку вектора вихря сквозь произвольную поверхность
S , опирающуюся на этот контур

где - циркуляция скорости,
м2/c; L - контур циркуляции; /dr/ = dL - направленный элемент контура; n - направление нормали к поверхности S; v - скорость,
м/с.
- циркуляция скорости,
м2/c; L - контур циркуляции; /dr/ = dL - направленный элемент контура; n - направление нормали к поверхности S; v - скорость,
м/с.
В 1870 г. французский кораблестроитель Жак Норман (1839-1906 гг.)
поставил вопрос о создании таких приближенных формул при проектировании судна, которые “позволят привести целый вопрос, иногда очень сложный, к одной или двум формулам, где легко можно будет увидеть влияние каждого элемента, например, веса корпуса или механизмов, расхода топлива или района плавания, толщины брони у бронированных кораблей” [2], что означало необходимость применения дифференциального исчисления в теории проектирования судов. В этом же году Норман опубликовал свои, получившие всемирную известность, приближенные формулы элементов теоретического чертежа.
a b /d
» 1,15 , (1870 г.)
где a - коэффициент полноты ватерлинии;
b - коэффициент полноты мидель-шпангоута;
d - коэффициент общей полноты.
В 1870 году опубликовывается и первая научная статья Степана Макарова (1848-1904 гг.), посвященная исследованию непотопляемости корабля на примере аварии канонерской лодки “Русалка”. Этот русский военный моряк и ученый считается основоположником теории непотопляемости корабля. В целом ряде научных работ 1870-1898 гг. Макаров проводит анализ непотопляемости отдельных кораблей, рекомендует метод модельного эксперимента для исследования непотопляемости, предлагает принцип контрзатопления отсеков для устранения аварийных крена и дифферента, составляет первые
таблицы непотопляемости. Ему принадлежит идея спрямления поврежденного корабля, основанная на равенстве кренящего и спрямляющего моментов.
 |
Краткая биографическая справка:
Степан Макаров, русский флотоводец и ученый, вице-адмирал, внесший значительный вклад в развитие океанологии, метеорологии, кораблестроения и военно-морской тактики, освоение Северного ледовитого океана. Окончил Морское училище в Николаевске-на-Амуре. С 1861 по 1872 гг. плавал на кораблях Сибирской флотилии и Тихоокеанской эскадры, работал над проблемами
непотопляемости и живучести корабля. Будучи командиром вооруженного парохода «Великий князь Константин» во время русско-турецкой войны 1877-78 гг. организовал и совершил первую в мировой практике успешную торпедную
атаку. С 1881 по 1904 гг. командовал различными кораблями и соединениями, Кронштадским портом и Первой Тихоокеанской эскадрой, внес большой вклад в становление русского Тихоокеанского флота. Участвовал в разработке кораблестроительных программ и совместно с Менделеевым технического задания на проектирование ледокола «Ермак». Погиб на броненосце «Петропавловск» во время Русско-Японской войны.
|
Время показало, что научные работы Макарова предопределили лидирующее положение русской корабельной науки в области теории непотопляемости судна. Острая необходимость разработки теории непотопляемости к концу XIX века объяснялась участившимися случаями гибели судов от разгерметизации корпуса и попадания в него большого количества воды не только в боевых условиях в результате поража-ющего воздействия мин и снарядов, но и в мирное время - чаще всего в результате столкновений. Это в особенности касалось военных кораблей, боевая эффективность которых должна сохраняться в течение всего боя.
В связи с этим можно привести в качестве примера целую серию крупнейших катастроф с боевыми кораблями, начиная с 60-годов XIX века. Гибель нескольких низкобортных казематных броненосцев конфедератов и башенных мониторов федералов в ходе гражданской войны в США 1861-65 гг.; в 1866 г. во время Лисского боя броненосных эскадр Австрии и Италии за 3 минуты исчезает с поверхности воды итальянский флагман "Ре д,
Италия", протараненный австрийским броненосцем "Фердинанд Макс"; в 1875 г. погибает английский броненосец "Вэнгард", также протараненный в тумане броненосцем "Айрон Дюк"; 1893 г. - гибель новейшего английского флагманского броненосца "Виктория" от тарана броненосца "Кампердаун" и невезучей русской канонерки "Русалка"; в 1897 г. в результате столкновения с необозначенным на картах подводным препятствием, несмотря на героические усилия экипажа, тонет новый русский броненосец "Гангут"; боевые итоги японо-китайской и американо-испанской колониальных войн на море 1894 и 1898 гг., в результате которых было потоплено значительное количество броненосных кораблей, главным образом, китайских и испанских.

Рис. 35. Флагманский английский броненосец “Кептен” (L= 97,5 м; B= 16,2 м; T= 7,8 м; D= 7891 т; v= 14,2 уз; N= 5400 л.с.) кораблестроителя К.Кольза. Опрокидывание этого корабля от резкого шквала ветра в 1870 г., в результате чего вместе с 473 членами экипажа погибает и его конструктор, выявило необходимость обеспечения не только начальной остойчивости, но и остойчивости на больших углах крена.
События 1870 г.
- Английский клипер “Патриарх” устанавливает рекорд скорости для парусных кораблей на линии Лондон - Сидней (через юг Африки), пройдя маршрут за 69 суток, который удалось улучшить только в 1975 г. английской яхте “Грейт Бритн II”.
- Английский изобретатель Чарльз Рамус создает проект глиссирующего миноносца.
- Лобовое столкновение парохода компании Инман лайн “Сити оф Бостон” с айсбергом, которое хоть и спасает судно, но приводит к многочисленным жертвам среди пассажиров и экипажа (191 человек погибшими).
В 1872 г. Фруд выдвигает гипотезу независимости составляющих
гидродинамического сопротивления, которая позволяет ему вскоре разработать методику определения сопротивления проектируемого судна с использованием модельных испытаний для получения волнового и вихревого сопротивления (сопротивления формы) как
остаточного. Проведя в 1874 г. натурную буксировку фрегата для проверки своей методики, Фруд окончательно отрабатывает и методику проведения натурных буксировочных испытаний судов.
События 1872 г.
- В России спущен на воду первый в мире брустверный броненосец-монитор “Петр Великий”, спроектированный выдающимся кораблестроителем Андреем Поповым (1821-1898 гг.).
- Во Франции спущен на воду первый барбетный броненосец “Адмирал Дюпре”.
- В России завершено проектирование первого в мире минного заградителя “Гальванер”, рассчитанного на 30 мин.
- В Николаеве ведется постройка первой круглой броненосной батареи А.Попова (“поповки”) “Новгород”, имеющей рекордное число гребных валов (6 гребных винтов).
- Впервые обладателем Голубой ленты Атлантики становится трансатлантический лайнер известной судоходной компании Уайт Стар лайн - пароход “Балтик” (BRT=3850 рег.т, v=14,8 уз), оснащенный впервые компаунд-машинами - паровыми машинами двойного действия.
- В Петербурге заканчивается строительство первого в мире броненосного крейсера (с парусным вооружением фрегата) “Генерал -Адмирал” (D=4600 т, v=13,2 уз) по проекту, разработанному кораблестроителями А.Поповым, И.Дмитриевым и Н. Кутейниковым.
- Вступил в строй роковой трансатлантический лайнер компании Уайт Стар лайн “Адриатик”(BRT=3850 рег.т, v=14,4 уз), обладатель Голубой ленты Атлантики: за всю 24-летнюю жизнь это судно перенесло четыре столкновения с другими судами.
- Переоборудование английского военного корвета “Челленджер” (D=2300 т, L=62,5 м, N=885 квт) в первое специальное научно-исследовательское судно и начало первой комплексной океанографической кругосветной экспедиции под руководством профессора Чарльза Томсона (1830-1882 гг.). За четыре года плавания судном было пройдено 68900 миль, организовано 362 океанографические станции, проведено большое количество промеров глубин и проб донных осадков.
- Австрийская арктическая экспедиция под руководством Карла Вайпрехта (1838-1881 гг.) на судне “Тегетгоф” открывает архипелаг Франца-Иосифа.
- В соответствии с решением арбитражного суда в Женеве Англия выплатила США 15,5 млн. долларов за возмещение убытков, нанесенных американскому торговому судоходству во время Гражданской войны в США 1861 - 1864 гг. крейсером конфедератов “Алабама”, который сумел потопить 68 торговых судов северян. Корвету федералов “Кирсардж” удалось потопить этот корабль у французского порта Шербур только в 1864 г.
- Загадка американского парусника “Мария Целеста”, обнаруженного в 600 милях к западу от Гибралтара английским бригом “Дея Грация”, на котором не было обнаружено ни одного члена экипажа при полных судовых запасах.
- Гибель со всем экипажем в результате внезапного опрокидывания от налетевшего шквала английского фрегата “Эвридик”, произошедшая на глазах у встречающей публики.
В 1873 г. французский инженер-кораблестроитель Жоссель исследует давно известный эффект подъемной или боковой силы пластины (позднее крыла), ориентированной под некоторым углом к набегающему потоку. Имитируя пластиной судовой руль, он впервые получает ее гидродинамические характеристики
в зависимости от, так называемого, угла атаки - угла между пластиной и набегающим потоком (рис.36). Через десять лет знаменитый французский инженер А. Эйфель, создатель радиобашни в Париже, проводя опыты с такими же пластинами, обнаружил, что подъемная сила формируется не столько давлением на нагнетающей поверхности, сколько разрежением на засасывающей и превышает первую в 2 - 3 раза. Таким образом были созданы все теоретические предпосылки для последующих исследований сначала крыла в аэродинамике, а затем и судна на подводных крыльях (СПК).
События 1873 г.
- Катастрофа налетевшего на скалы Галифакса английского пассажирского лайнера “Атлантик” (BRT=3850 рег.т) компании Уайт Стар, которая оставалась самой крупной в пассажирском судоходстве вплоть до гибели в 1912 г. печально известного “Титаника” этого же судовладельца: тогда из 952 пассажиров, находящихся на борту, погибло 585 человек.
В связи с гибелью в 1874 г. английского железного парохода “Мэри” длиной 64 м, разломившегося пополам во время перехода через Атлантический океан из-за потери устойчивости палубного настила, в Англии был разработан способ подсчета элементов продольных связей корпуса в так называемом втором приближении. По предложению инженера
Джона критическое напряжение определялось по Рэнкину как для балки-полоски с заделанными концами и производилось редуцирование (условное уменьшение) площади сечения сжатых пластин. Однако это ценное предложение Джона почему- то не привлекло к себе в свое время внимание.
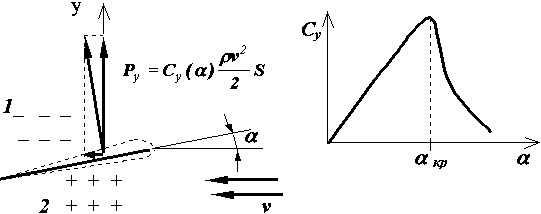
Рис. 36. Эффект подъемной силы и ее гидродинамическая характеристика. 1 - зона разряжения; 2 - зона повышенного давления; a - угол атаки; Ру - подъемная сила; Су - коэффициент подъемной силы; S - площадь пластины.
В 1876 г. после упорной восьмилетней борьбы в английском парламенте крупным судовладельцем Самюэлем Плимсолем проводится, так называемый, “Билль о надводном борте”, регламентирующий минимальный надводный борт и грузовую марку (круг Плимсоля). Этот закон, являющийся прообразом современных “Правил о грузовой марке”, стал еще одним вкладом в повышение безопасности эксплуатации гражданских судов за счет обеспечения минимального запаса плавучести.
Fmin = f(L, lн , sп) , (1876 г.)
где L - длина судна; lн - длина надстроек; sп
- седловатость палубы.
События 1876 г.
- Немецкий инженер Николаус Отто (1832-1891 гг.) создает первый двигатель внутреннего сгорания с предварительным сжатием топлива - бензиновый мотор.
- Во Франции спущен на воду первый стальной броненосец “Редутабль” (D=9500 т).
- Во Франции построен самый большой за всю историю судостроения деревянный броненосец “Ришелье” водоизмещением 9100 т (L=101,7 м).
- Датчанин А. Энсен первым в одиночку пересек Атлантический океан на рыбацком боте “Сентенниэл” длиной всего 6 метров.
- Третий год идут Карские экспедиции русских пароходов по Сев. морскому пути до устьев Оби и Енисея, финансируемые русским предпринимателем, золотопромышленником и исследователем Сибири Александром Сибиряковым (1849-1933 гг.), за всю историю которых было осуществлено 122 рейса и 75 из них завершились благополучно.
- Русский военный моряк Александр Можайский (1825-1890 гг.) создает проект воздухоплавательного аппарата, который был по-корабельному настолько тяжел, что так и не поднялся в воздух во время испытаний в 1882 г.
- Русский ученый, один из основоположников современной теории девиации магнитного компаса, Иван де Колонг (1839-1901 гг.) испытывает первый в мире дефлектор - прибор для измерения и компенсации полукруговой и креновой девиации, и разрабатывает методы расчета и компенсации четвертной девиации, которые вскоре были приняты на вооружение во всех флотах мира.
 |
Краткая биографическая справка:
Степан Джевецкий, русский инженер и изобретатель, лауреат Международного конкурса в Париже 1898 г., руководитель воздухоплавательного отделения Русского технического общества, внесший большой вклад в развитие кораблестроения и воздухоплавания. Автор множества проектов подводных лодок, в том числе первой серийной подводной лодки и подводной лодки «Почтовый» с единым бензиновым двигателем для русского военно-морского флота. Разработчик проектов «водобронного» миноносца и различных вооружений для подводных лодок, механического прибора для автоматической прокладки курса корабля на карте.
|
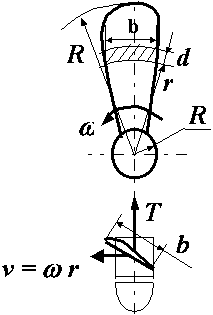
Рис.37. Схема лопастной теории гребного винта.
В 1878 г. Фруд предлагает первую лопастную теорию гребного винта, которая затем в 1892-1900 гг. была развита выдающимся русским инженером Степаном Джевецким (1843-1938 гг.) - автором проекта первой серийной подводной лодки в России. Эта теория была основана на исследованиях подъемной силы пластины или крыла и явилась значительным шагом вперед по сравнению с используемой до этого схемой идеального движителя (рис.37).
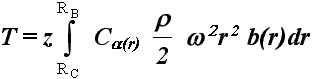 , (1878 г.)
, (1878 г.)
где Т - тяга винта, н; z - число лопастей винта; RC
и RB - cоответственно, радиусы ступицы и винта, м; Ca(r)-
коэффициент подъемной силы на элементе лопасти с углом атаки
a и текущим радиусом r ; r - плотность воды,
кг/м3; w - частота вращения гребного винта,
рад/c; r - текущий радиус винта, м; b(r) - ширина лопасти винта, м.
События 1878 г.
- В Швеции по проекту инженера Людвига Нобиля (1831-1888 гг.) для каспийских нефтепромыслов построен первый в мире самоходный танкер “Зороастр” (D=400 т, L=56 м, v=10 уз).
- В Англии построены первые в мире военные корабли из мягкой судостроительной стали: двухвинтовой крейсер “Айрис” с ограниченным парусным вооружением (D=3700 т, v=18,5 уз) и бронепалубный крейсер “Комус” (D=2380 т, v=13 уз).
- В России на заводе Берда спущен на воду первый в мире миноносец “Взрыв” водоизмещением 134 т и скоростью 15 уз.
- В Англии проходит испытания первая быстроходная миноноска с носовым торпедным аппаратом под торпеды Уайтхэда.
- Дж.Эриксон строит за свой счет водобронный миноносец “Дистройер” (L=40 м), испытания которого не оправдали возлагавшихся на этот тип корабля надежд.
- Шведский полярный исследователь Нильс Норденшельд (1832-1901 гг.) на судне “Вега” начал плавание в восточном направлении по Сев. морскому пути и прошел его с одной зимовкой на Чукотке, вернувшись в Швецию через Суэцкий канал.
- В Глазго построен танкер-парусник “Фоллс оф Клайд” (L=81 м), сохранившийся до наших дней (Гонолулу).
- Первая в мире боевая торпедная атака во время русско-турецкой войны 1877-1878 гг. турецкого парохода “Интибах” минными катерами “Чесма” и “Синоп” под командованием С. Макарова, закончившаяся потоплением парохода на Батумском рейде и открывшая эпоху применения торпед в военно-морском деле.
- По международному соглашению за меридиан отсчета времени по широте принят меридиан астрономической обсерватории в английском городе Гринвич вблизи Лондона.
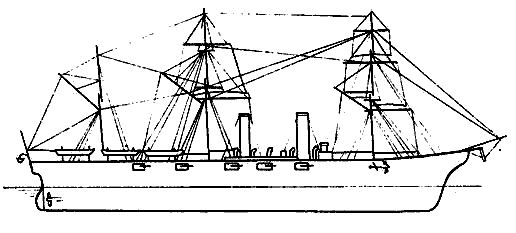
Рис.38. Английский стальной быстроходный двухвинтовой крейсер “Айрис” (L= 101,5 м; B= 14 м; T= 6,7 м; D= 3750 т; v= 18,6 уз; N=7500 л.с.), при испытаниях которого в 1878 г. выявилась необходимость проектирования оптимального винта. После невыполнения на сдаточных ходовых испытаниях контрактной скорости на один узел и замены четырехлопастных винтов двухлопастными сдаточная комиссия была буквально ошеломлена: если с четырехлопастными винтами при мощности машин 5250 л.с. корабль показывал 15,1 уз, то с двухлопастными - уже при мощности 4370 л.с. он развил скорость 15,5 уз.
В 1880 г. издается научный труд выдающегося русского ученого Дмитрия Менделеева (1834-1907 гг.) “О сопротивлении жидкости и о воздухоплавании”,
в котором, в частности, обобщаются все научные достижения того времени в области гидродинамики судна и дается понятие пограничного слоя жидкости. Исследуя критически опыты Фруда, Менделеев предлагает учитывать шероховатость поверхности при определении сопротивления трения. Впоследствии многие ученые - гидродинамики будут уделять этому вопросу большое внимание, так как от шероховатости обтекаемой поверхности зависят толщина пограничного слоя и его характер, определяющие, наряду с формой корпуса, вязкостное сопротивление судна в целом.
Fтр = Fтр.o + D Fтр.ш
, (1880 г.)
где Fтр - полное сопротивление трения воды о поверхность корпуса судна; Fтр.o - сопротивление трения технически гладкой поверхности;
D Fтр.ш - надбавка к сопротивлению трения, учитывающая шероховатость поверхности.
Краткая биографическая справка:
Дмитрий Менделеев, русский ученый, открыватель периодического закона химических элементов. Окончил Главный педагогический институт в Петербурге, член Петербургской АН, автор свыше 500 работ в области химии и химической технологии, физики, метрологии, воздухоплавания и гидроаэродинамики, метеорологии, сельского хозяйства, экономики, народного просвещения, кораблестроения и мореплавания. Заложил основы теории растворов, предложил промышленный способ перегонки нефти, изобрел вид бездымного пороха, один из инициаторов создания Русского химического общества, организатор и первый директор Главной палаты мер и весов. Один из первых в России предложил строить нефтеналивные суда, руководил проводившимися на флоте экспериментами по исследованию сопротивления воды и ходкости кораблей, обосновал необходимость создания в России опытового бассейна, предложил широкую программу государственных мероприятий по развитию технической базы отечественного судостроения, занимался вопросами перевода судов на жидкое топливо. Обосновал народно-хозяйственное и оборонное значение Северного морского пути и постройку
первого в мире арктического ледокола, совместно с Макаровым разработал техническое задание на проектирование ледокола “Ермак”.
|
 |
События 1880 г.
- К Северному полюсу дрейфует американская яхта “Жанетта” полярного исследователя Джорджа де Лонга (1844-1881 гг.), которая в 1881 г. будет раздавлена льдами и затонет.
- Русский инженер С. Джевецкий разработал проект первой в мире подводной лодки с электрическим двигателем, работающим от аккумулятора.
- В Англии строится первый цитадельный броненосец “Инфлексибл”, имеющий броневую палубу в средней части и спроектированный пришедшим на смену Э.Риду главным кораблестроителем Натаниелем Барнаби (1829-1915 гг.), основателем Английского общества корабельных инженеров.
- В Италии спущен на воду самый большой железный боевой корабль - крейсер-броненосец “Италия” (D=15200 т, v=18 уз), который явился и первым шеститрубным кораблем.
- В США постройкой первой четырехмачтовой шхуны “Вильям Уайт” начинается строительство гигантских многомачтовых гафельных шхун, которое завершится появлением в 1900 г. шестимачтовой “Джорж Уэллс” и в 1902 г. - семимачтовой шхуны “Томас Лаусон”. Последняя стала знаменитой не столько как единственный в истории судостроения семимачтовый парусник, сколько своей поразительной гибелью: по иронии судьбы эта шхуна разбилась о камни в пятницу 13 ноября 1907 г. - в полном соответствии с названием романа американского писателя (“Пятница - 13 число”), имя которого носил корабль.
В 1883 г. английский ученый Осборн Рейнольдс (1842-1912 гг.) экспериментально получил еще один важный критерий гидродинамического подобия, представляющий собой отношение сил инерции к силам вязкости и широко используемый в практике судостроения.
Re = v L / n , (1883 г.)
где Re - число Рейнольдса; v - скорость потока жидкости или движения тела в ней, м/c; L - длина или прочий характерный геометрический размер тела,
м; n - кинематический коэффициент вязкости,
м2/c.
Исследуя пограничный слой жидкости, он пришел к выводу, что сопротивление трения ее о стенки твердого тела зависит от характера течения жидкости. В зависимости от него он предлагает разделять пограничный слой на ламинарный и турбулентный
(рис.39).

Рис.39. Линии тока и эпюры скоростей в ламинарном и турбулентном пограничном слое. 1 - ламинарный пограничный слой; 2 - турбулентный пограничный слой; 3 - толщина пограничного слоя; 4 - эпюра скорости линий тока; 5 - линии тока ламинарного пограничного слоя; 6 – эпюра средней скорости турбулентного потока; 7 – вихри турбулентного пограничного слоя.
В том же году английский корабельный инженер А. Денни на основании исследований Э. Рида впервые предлагает критерии нормирования остойчивости для небольших грузовых судов. Это явилось важным событием в развитии гражданского судостроения, так как такие суда, в общем, любого назначения, также зачастую гибли от потери остойчивости. Позднее ученые выяснят, что вероятность опрокидывания небольшого судна гораздо больше, чем большого, и обеспечение остойчивости малых судов носит в целом более сложный характер.
События 1883 г.
- Шведскому инженеру-механику Карлу Лавалю (1845-1913 гг.) выдан первый патент на паровую турбину, которую он смог построить и испытать на лодке только в 1893 г.
- Английский инженер-кораблестроитель Торникрофт заканчивает строительство и испытывает винтовую и водометную миноноски водоизмещением по 14,5 т, которые окончательно показали преимущества гребного винта: скорость водометной миноноски оказалась аж на 30% меньше, чем у винтовой, в результате чего водомет надолго выбыл из арсенала средств борьбы за скорость.
- Трансатлантический лайнер компании Гийон лайн “Орегон” (BRT=7400 рег.т), на котором впервые оборудовано электрическое освещение, на испытаниях показывает небывалую скорость 20 уз и становится в первом же рейсе обладателем Голубой ленты, пройдя дистанцию со средней скоростью 18,4 уз.
В 1884 г. по результатам трагической гибели в 1870 г. у м. Финистерре новейшего английского броненосца “Кептен”, имевшего низкий надводный борт монитора и полное парусное вооружение корабля, главный конструктор ВМС Англии Эдвард Рид (1830-1906 гг.) опубликовывает свой фундаментальный научный труд “Стабильность (остойчивость) кораблей”, где представлена диаграмма остойчивости судна на больших углах крена, которая с тех пор носит название диаграммы Рида. В этой книге показано, что “Кэптен” (рис.35), построенный кораблестроителем Купером Кользом, при динамическом действии шквала опрокидывается уже при 12-130 крена, тогда как для броненосца Рида “Монарх” эта опасность начинается только с 23
0 (рис.40).

Рис.40. Определение опрокидывающего момента и соответствующего ему угла крена по диаграмме Рида.
Значение исследований Рида по остойчивости судов было огромно, ибо они уже в ближайшее время дадут свои плоды, сохранив жизнь многим поколениям моряков во всем мире. Казалось бы, что проблема обеспечения остойчивости, сопутствующая развитию кораблестроения с самого его зарождения, наконец может быть снята. Тем не менее опрокидывание судов от потери остойчивости до сих пор является основной причиной их гибели, что требует от корабельной науки дальнейших усилий в этом направлении.
В этом же году французский ученый Морис Леви (1838-1910 гг.), ученик основоположника теории пластичности Сен-Венана, впервые решает задачу устойчивости цилиндрической оболочки на примере кольца, определив ее критическую нагрузку на разных стадиях потери устойчивости от наружного равномерного давления
 ,
,
где qкр - критическая погонная нагрузка, т/м; r - радиус кольца, м; n - число волн кольца, потерявшего устойчивость (рис.41).
*) По многим
источникам - "Наутилус". |
В отличие от котельной формулы, формула Леви имела чисто корабельную природу, отвечая запросам развивающегося подводного кораблестроения. К этому времени среди конструкторов подводных лодок окончательно укореняется мнение о круговой форме ее прочного корпуса как оптимальной по материалоемкости. Несмотря на то, что попытки использования формы прочного корпуса в виде тел вращения предпринимались еще с начала XIX века ("Наутиль 2"* Фултона, 1801 г.; подводная лодка К. Чарновского, 1825 г.), поиски оптимальной формы велись вплоть до 1860 г., так как в соответствии с тогдашней концепцией "ныряющей лодки" считалось, что ее корпус должен быть подобен корабельному.

Рис. 41. Расчетная схема сжатого снаружи кольца и формы потери его устойчивости.
С увеличением в этот период глубины погружения подводных лодок с 2 до 15 м к концу XIX века участились и их аварии из-за разрушения прочного корпуса. Наиболее трагичными считаются случаи гибели в 1851 г. сразу двух подводных лодок - "Брандтаухера" В. Бауэра водоизмещением 38,5 т, которая была раздавлена давлением на глубине 18 м, и паромашинной лодки американца Лоднера Филиппса во время погружения на о. Эри. В последнем случае подводная лодка, превысив расчетную глубину, похоронила на дне озера экипаж вместе с ее изобретателем. Не исключено, что и "Умный кит" ("Интеллижент уэйл") американца О. Халстеда за время беспрецедентных десятилетних испытаний с 1862 по 1872 год неоднократно затапливался из за разрушения корпуса под действием давления, так как за этот период с его помощью было отправлено на тот свет 39 человек.
Не случайно, что именно во Франции, имеющей лучшую в Европе научную школу строительной механики, в 80-годах XIX века ведутся интенсивные поиски не только надежного двигателя для подводной лодки, но и оптимальной формы ее прочного корпуса, в результате чего к началу XX века она занимает лидирующее положение в подводном кораблестроении.
События 1884 г.
- Английский инженер-механик Чарльз Парсонс (1854-1931 гг.) патентует многоступенчатую реактивную паровую турбину, которая уже к концу 20 века начнет повсеместно применяться в качестве главного двигателя на боевых кораблях развитых морских держав.
- На верфи “Томсон” в Глазго для компании Нэшнл лайн построен первый стальной трансатлантический лайнер “Америка”, дважды завоевавший Голубую ленту Атлантики со средней скоростью 17,5 уз.
- В Глазго открыт Департамент судостроения - главное кораблестроительное учебное заведение Шотландии.
В 1885 г. Норман опубликовывает научный труд, в котором, используя дифференциальный метод, показывает, что водоизмещение проектируемого судна растет значительно быстрее веса, который в силу изменения задания на проектирование судна добавляется к весам по отдельным разделам нагрузки судна-прототипа. Отношение приращения водоизмещения к приращению веса по статьям нагрузки отныне получило название коэффициента Нормана.
 , (1885 г.)
, (1885 г.)
где h н - коэффициент Нормана;
D D - приращение водоизмещения;
D P - приращение весов; ¶
P(D)/¶ D - частная производная уравнения нагрузки по водоизмещению.
Дифференциальная форма уравнения весов Нормана имела в свое время большое практическое значение для проектирования судов, так как позволяла при любом изменении в нагрузке проектируемого корабля быстро получить новое значение водоизмещения, не пересчитывая каждый раз уравнения весов в алгебраической форме. Постоянно меняющиеся в те времена интенсивного строительства боевых кораблей (во Франции Норман специализировался на проектировании и строительстве миноносцев) условия поставки материалов и оборудования, машинной установки и боевых вооружений для проектируемых кораблей предопределили научные изыскания этого талантливого кораблестроителя по совершенствованию уравнения нагрузки.
События 1885 г
- В Англии ведется подготовка к строительству первых океанских бронепалубных броненосцев “Трафальгар” и “Нил”, которые послужили прототипами для целого поколения броненосцев во всем мире на протяжении 15 - 20 лет.
- В Швеции идет строительство первой стальной подводной лодки водоизмещением 160 т по проекту инженера Норденфельда, вооруженной двумя торпедами Уайтхэда и приводимой в движение паровой машиной.
- На заводе Ярроу (Великобритания) по заказу Японии идет строительство первого бронированного миноносца “Котака” (D=190 т, v=19 уз).
- В Англии ведется строительство первого океанского танкера “Глюкауф” дедвейтом 3 тыс.т.
- С. Джевецкий на своей подводной лодке впервые испытывает водометный движитель с электроприводом.
- Французский инженер Клод Губе проектирует и строит свою первую подводную лодку, которая была признана неудачной и не принята морским министерством.
В 1889 г. в результате многолетних исследований ходовых испытаний кораблей, выдающийся русский инженер-механик флота Василий Афанасьев (1843-1913 гг.)
предлагает метод, так называемых, адмиралтейских коэффициентов, позволяющий достаточно точно прогнозировать ходовые качества корабля, не прибегая к испытаниям в опытовом бассейне, и выраженный простой эмпирической формулой, ставшей поистине знаменитой
N = D 2/3 v3 / CА о
или в общем виде
N = D m v n / Co
, (1889 г.)
где N - мощность главных двигателей, л.с. или квт; D - весовое водоизмещение судна, т; v - скорость хода, уз; САо - адмиралтейский коэффициент.
 |
Краткая биографическая справка:
Василий Афанасьев, русский инженер-механик флота, ученый, генерал-лейтенант. Окончил Инженерное и артиллерийское училище в Кронштадте и Академический курс морских наук по механическому отделу, преподавал в Штурманском и артиллерийском училище Кронштадта, работал на Кронштадском пароходном заводе, старшим помощником главного инспектора механической части Морского технического комитета. Автор научных работ по прочности, электромагнетизму, проектированию судов и судовым энергетическим установкам. Инициатор иссследований ходкости и создания ледоколов в России.
|
Значение метода Афанасьева действительно трудно переоценить, особенно с точки зрения проектирования судов. Со времен обобщенного уравнения весов Окунева, куда вошли составляющие нагрузки в функции водоизмещения, связанные с мощностью главных двигателей, никому еще не удавалось такой простейшей и достаточно точной для первого приближения формулой связать потребную мощность главных двигателей с водоизмещением и скоростью хода. Можно сказать, что эта формула завершила формирование современного уравнения нагрузки в теории проектирования судов с механическими двигателями и сразу же нашла повсеместное применение в мировой практике судостроения. Достаточно привести высказывание А. Крылова: “Эта формула, замечательная по своей простоте и точности, вскоре вошла во всеобщее употребление, сводя вычисления, требующие затраты многих часов, к нескольким минутам” [26].
Исследования Афанасьева по ходкости кораблей были опубликованы в научной работе “Материалы к изучению движения судна”, изданной в 1899 г. В ней, в частности, он впервые использует понятие “боевой скорости судна”, исследует условия совместной работы винта с корпусом корабля, предлагает не менее замечательную эмпирическую зависимость между скоростью корабля и числом оборотов движителя.
События 1889 г.
- С. Макаров выдвигает идею применения на боевых кораблях комбинированной энергетической установки, включающей главные двигатели форсированного и экономичного хода, реализованную только в 1897 г. на крейсере “Россия”.
- Русский горный инженер Николай Славянов (1854-1897 гг.) демонстрирует “плавильник” - первый в мире полуавтомат дуговой сварки металлическим электродом, - и использует его впервые в мировой практике при постройке в Перми буксирного парохода “Редедя, князь Косогорский”.
- Английский военно-морской теоретик и историк Филип Коломб (1831-1899 гг.) разрабатывает рекомендации по предупреждению столкновений судов в море, которые были приняты во всем мире как первые обязательные правила.
- В порту Апиа в Зап. Самоа в результате тайфуна погибли шесть боевых кораблей США и Германии, а также множество местных судов прибрежного плавания.
- Французский инженер Густав Зеде (1825-1891 гг.) заканчивает комплексные испытания подводной лодки “Жимнот” (D=31 т) с единым электрическим двигателем на аккумуляторной батарее, которая была построена по проекту Дюпюи де Лома.
- Русский военный моряк Владимир Степанов (1858-1904 гг.) работает над проектом мореходного минного заградителя, на основании которого по инициативе С.Макарова в России в 1892 г. будут построены первые корабли этго класса “Буг” и “Дунай”.

Рис. 42. Первая боевая электрическая подводная лодка французского инженера Густава Зеде "Сирена" * (L= 45,1 м; D= 266/272 т; v= 12/10 уз; N= 360 л.с.), построенная в 1893 г., вероятно является и первой лодкой, при проектировании которой предпринимались попытки проверки прочного корпуса на устойчивость (рабочая глубина 17 м).
В 1894 г. Рид, который еще в 1870 г. предложил рабочую методику расчета общей продольной прочности корабля, и английский ученый Стенбюри математически обосновано установили, что корпус судна при общем изгибе ведет себя подобно простой балке. С этого момента повсеместно при проверке корпуса судна на общую продольную прочность используется, так называемый, эквивалентный брус (рис.43).
С разработкой методики проверки общей продольной прочности по эквивалентному брусу в целом была сформирована методология обеспечения этого важного эксплуатационного свойства судна в том виде, в котором она существует и поныне.
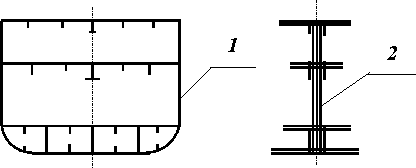
Рис. 43. Эквивалентный брус корпуса корабля: 1 - поперечное сечение корабля; 2 - эквивалентный брус корабля.
В этом же году выходит в свет фундаментальный труд немецкого ученого Отто Шлика, посвященный систематическим исследованиям вибрации судов - негативного явления, которое давно начало преследовать суда, оснащенные, в первую очередь, паровыми машинами, и особенно после того, как их корпуса стали металлическими. Появление гребного винта с его высокочастотными периодическими нагрузками еще более усугубило остроту проблемы борьбы с вибрацией корпуса.
Низкочастотная вибрация корпусных конструкций от работы паровых машин на деревянных пакетботах и пароходофрегатах настолько сильно ускоряла процесс разгерметизации всего корпуса, что явилась, в конце концов, одной из причин использования на мощных пароходах железных корпусов. Однако вскоре оказалось, что металл является значительно более лучшим проводником волновых колебаний, чем дерево, что привело к появлению
структурной вибрации всего металлического корпуса, особенно после перехода к более изящным стальным конструкциям.
Замена гребного колеса винтом в корме добавила кораблестроителям проблем - появляется еще и локальная вибрация оконечности судна и чем несовершенней винт, тем она становится больше. Если к тому же добавить периодически вызываемую вибрацию носовой части корпуса от ударов волн, можно себе представить всю полноту этой проблемы: сильная вибрация не только расшатывает конструкции и механизмы, она плохо влияет на самочувствие человека, а на боевом корабле - не позволяет эффективно использовать и оптические приборы для наведения орудий.
События 1894 г.
- Немецкая фирма Крупп завершает процесс создания совершенной цементированной хромо-никелевой броневой стали.
- Эксплуатация во Франции первого судна с алюминиевым корпусом - яхты “Венденессе” (D=15 т).
- Немецкий инженер-механик Рудольф Дизель (1858-1913 гг.) создает первый опытный образец нового запатентованного им двигателя внутреннего сгорания - дизеля, который в настоящее время является самым распространенным типом судового двигателя.
- В России вступил в строй первый в мире большой броненосный крейсер “Рюрик” (D=10950 т), преодолевший десятитысячный рубеж водоизмещения.
- В Англии вступает в строй броненосец “Маджестик”, схема бронирования которого вскоре стала использоваться во всех флотах мира: бортовая палуба корабля имела скосы к нижней кромке бортовой поясной брони.
- Инженер-механик русского флот Павел Кузьминский (1840-1900 гг.) создает первую газотурбинную установку для катера, однако его испытания не были завершены в связи со смертью изобретателя.
- Обладателем Голубой ленты Атлантики становится величественный кунардовский лайнер “Лукания” (BRT=12500 рег.т, v=22 уз), на котором впервые установлены паровые машины тройного расширения мощностью 30 тыс. л.с., работающие на два гребных вала.
- На итальянской подводной лодке инженера Пуллино “Дельфино” (D=95 т) впервые установлен перископ.
- В Петербурге начал функционировать первый русский опытовый бассейн, созданный после того, как в 1888 г. русский броненосец, на котором находился великий князь Алексей Александрович, был обогнан английским кораблем такого же класса.
- Ялуцзянский бой между китайской (Дин Чужан, 14 кор) и японской (Ито, 12 кор) эскадрами во время японо-китайской войны 1894 -1895 гг., который закончился поражением китайцев, потерявших потопленными 4 корабля.

Рис. 44. Английский истребитель миноносцев (контрминоносец) “Дэринг” (L= 56,6 м; B= 5,7 м; T=2,1 м; D= 264 т) впервые столкнулся с явлением кавитации гребных винтов, развив на сдаточных испытаниях в 1894 г. скорость 24 уз вместо 27 контрактных. В результате смены на этом истребителе шести пар гребных винтов, в конце концов, корабль достиг желаемой скорости с винтами, имеющими на 45 % большую площадь лопастей, чем первоначально.
В 1896 г. выдающийся русский кораблестроитель и ученый Алексей Крылов (1863-1945 гг.) разрабатывает линейную гидродинамическую теорию килевой качки на волнении, а в 1898 г. - общую теорию совместной килевой и бортовой качки при движении корабля косыми курсами. Последняя теория была основана на гипотезе “проницаемости” корпуса судна для воды: на каждый элемент смоченной поверхности судна должно действовать такое давление, которое наблюдается в соответствующей точке волнующейся жидкости при отсутствии судна.
 |
Краткая биографическая справка:
Алексей Крылов, русский ученый-кораблестроитель, механик и математик. Окончил морское училище и кораблестроительное отделение Морской академии, член Петербургской АН и АН СССР, автор работ по теории корабля и строительной механике, теории магнитных и гироскопических компасов, артиллерии, механике, математике, истории науки. Разработал теорию вибрации корабля, создал ряд корабельных и артиллерийских приборов, руководил первым опытовым бассейном. Главный инспектор кораблестроения и председатель Морского технического комитета, участник проектирования и постройки первых русских линкоров типа “Севастополь”
и других кораблей, активный участник решения основных технических вопросов военного и гражданского судостроения в СССР, начальник Морской академии.
|
Таким образом, в отличие от теории Фруда гипотеза Крылова уже позволяла учитывать влияние формы корпуса на качку корабля. Для математического описания движения судна в пространстве Крылов использовал более удобную корабельную систему эйлеровых углов, которая применяется в теории корабля с небольшими изменениями до сих пор (см. рис. 27 б).
События 1896 г.
- Первое паротурбинное экспериментальное судно Ч.Парсонса “Турбиния” (D=44 т,L=30 м,N=2100 л.с., 3 гребных вала, 9 винтов) после неоднократных переделок на испытаниях показывает небывалую для того времени скорость 34,5 уз.
- В Нью-Йорке основано Американское Бюро Судоходства (АБС).* Мировой тоннаж металлических судов сравнялся с тоннажем деревянных судов.
- На испытаниях французский миноносец “Форбен” впервые преодолевает 30-узловый рубеж скорости, показав скорость 31 уз, и открывает соревнование “30-узловых” под девизом “любой ценой”, которое окажется роковым для паровой машины.
- Заканчивается постройка на заводе “Вулкан” в Штеттине гигантского пассажирского лайнера “Кайзер Вильгельм дер Гроссе” (BRT=14350 рег.т, v=22,8 уз), условием сдачи которого компании Норддойчер Ллойд впервые являлся переход через Атлантику за указанное в задании на проектирование судна время: в 1897 г. он становится первым германским обладателем Голубой ленты, пройдя дистанцию за 5 суток 20 часов.
- Французский инженер К. Адер начинает постройку экспериментального катера на воздушной подушке “Авион-3”, который в 1897 г. прошел успешные испытания.
- Русский электротехник Александр Попов (1859-1906 г.) на расстояние 250 м передает первую в мире радиотелеграмму: “Генрих Герц”.
- Закончился 3-летний дрейф в Арктике норвежского экспедиционного судна Фритьофа Нансена (1861-1930 гг.) “Фрам” с целью достижения Северного полюса.
- Подготовка и захват германской эскадрой Альфреда Тирпица (1849-1930 гг.) китайского порта Циндао, ставшего военно-морской базой тихоокеанской эскадры адмирала фон Шпее во время первой мировой войны.
- Зимовка в Антарктиде норвежского матроса с китобойного судна “Антарктик” Карстена Борхгревика (1864-1934 гг.) - первого исследователя, ступившего на этот континент.
В 1898 г. выдающийся русский ученый Николай Жуковский (1847-1921 гг.),
основоположник современной аэродинамики, вносит существенный вклад и в развитие гидравлики. Исследуя движение жидкости в трубах, он впервые физически обосновывает явление гидравлического удара, а также вырабатывает рекомендации по предотвращению этого негативного явления в эксплуатации систем.
D p = r
C v , (1898 г.)
где D p - максимальное приращение давления в жидкости, вызванное гидравлическим ударом, н/м2; r
- плотность жидкости, кг/м3; v - скорость течения жидкости по трубе, м/c; С - скорость распространения волны, равная скорости звука в жидкости, м/c.
Примерно в это же время, изучая сопротивление движению судна в воде, Жуковский впервые высказывает мысль об оптимальном соотношении параметров формы корпуса судна и его скорости хода: “Всякое очертание подводной части судна строго соответствует некоторой соответствующей для него наивыгоднейшей скорости движения; ... уклонение от этого очертания при данной скорости и, наоборот, уклонение от наивыгоднейшей скорости при данном обводе неизбежно влекут за собой быстрое возрастание сопротивления и бесполезно затрачиваемой работы” [26].
Необходимо также отметить вклад, который внес Жуковский в это время в развитие теории водометного движителя. Рассмотрев взаимодействие корпуса судна с этим движителем, он доказал его эффективность в широком диапазоне скоростей и упоров.
Краткая биографическая справка:
Николай Егорович Жуковский, русский ученый, основоположник современной аэродинамики. Окончил Московский университет, член Петербургской АН, автор работ по гидроаэродинамике, теории авиации, механике твердого тела, астрономии, математике, гидравлике, прикладной механике, теории регулирования машин и механизмов, реактивным движителям, теории корабля. Создал одну из первых в Европе аэродинамических
труб, основатель и первый руководитель аэродинамического института.
|
 |
В том же 1898 году в Лондоне издается научная работа австралийского ученого-гидродинамика
Джона Мичелла, в которой дается законченное математическое решение задачи о волновом сопротивлении корабля с узким корпусом в неограниченном фарватере (для идеальной жидкости), позволяющее перейти к аналитическому определению этой составляющей сопротивления. До этого волновая составляющая сопротивления в соответствии с методикой Фруда не выделялась даже экспериментальным путем, входя в остаточное сопротивление.
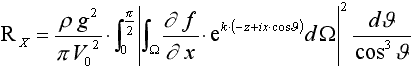 , (1898 г.)
, (1898 г.)
где Rx – продольное волновое сопротивление по оси Х, Н; f=f(x,z) – ординаты поверхности корпуса в функции абсцисс Х и аппликат Z, м; V0
– cкорость судна, м/с; Ω – площадь элементарной площадки на поверхности корпуса, м2; θ = arcos (V/V0) – фазовый угол Кельвина, задающий направление отраженных от корпуса волн, рад; V – скорость распространения корабельной волны в направлении θ, м/с; k = g/(V02 cos2
θ) – частота формы волны, 1/м (g – ускорение свободного падения, м/с2); i = (-1)0,5- мнимая единица.
События 1898 г.
- В Англии идет строительство первых боевых турбинных кораблей - четырехвальных и восьмивинтовых миноносцев “Вайпер” и “Кобра” (D=380 т,N=12 тыс.л.с.), которые в 1899 г. на испытаниях показали рекордную для того времени скорость 36,5 уз.
- Разрушение алюминиевого корпуса французской миноноски “Ля Фудр” (D=9,5 т,v=20,5 уз), давшего по сравнению со стальным 50% выигрыш в весе, от химической коррозии в морской воде.
- В Клайде для компании Уайт Стар лайн строится пассажирский лайнер “Океаник” (D=28500 т, BRT=17040 рег.т, L=214,7 м), который в XIX веке наконец-то превзошел по длине знаменитый брунелевский “Грейт Истерн”.
- В Англии построено первое судно для навалочных грузов “Юниверс”, имеющее конструкцию трюмов, которая позволяла исключить опасное смещение во время плавания и штивку во время разгрузки сыпучего груза.
- Сдан английскому Адмиралтейству со скоростью 31 узел самый мощный истребитель “Экспресс” (N=9250 л.с.), который проектировался под контрактную скорость 32-33 уз и окончательно выявил кризис паровой машины на кораблях этого типа.
- Подрыв и затопление американского броненосца “Мэн” (D=6648 т, L=94,5 м, v=17 уз) на рейде Гаваны, послуживший поводом к испано-американской войне.
- Американский капитан Джошуа Слокам (1844-1909 гг.) в возрасте 51 год завершает на шлюпе “Спрей” первое в истории одиночное кругосветное плавание, начавшееся в 1895 г.
- Бой в Манильской бухте во время американо-испанской войны 1898 г. американской (6 кор) и испанской (10 кор) эскадр, в результате которого все испанские корабли были потоплены.
- Норвежский исследователь Арктики, сподвижник Нансена, Отто Свердруп (1854-1930 гг.) начинает трехлетнее плавание на “Фраме” по северной части Канадского Арктического архипелага.
- Бой у Сантьяго-де-Куба американской (В. Сэмпсон, 8 кор) и испанской (П.Сервер, 6 кор) эскадр, закончившийся поражением испанцев и окончательным подрывом коммуникаций между Испанией и Кубой.
- В Блэкпуле сожжены останки прославленного английского 84-пушечного линейного корабля “Фудроян” (D=3500 т, L=66,8 м), прослужившего на флоте около 100 лет. Построенный в 1798 г. по образцу одноименного французского линейного корабля, захваченного англичанами в 1758 г., корабль до 1815 г. участвовал во многих боевых операциях английского флота и пленил три французских корабля. В 1892 г. он был продан на слом в Германию, но под давлением общественности выкуплен, возвращен в Англию и отреставрирован, однако в 1897 г. во время сильного шторма корабль выбросило на берег, после чего восстановление его оказалось невозможным.

Рис. 45. Обладатель Голубой ленты Атлантики - шикарный немецкий трансатлантический лайнер “Дойчланд” (L= 208,6 м; B= 20,4 м; T= 8,84 м; v= 23,5 уз; N= 36000 л.с.), сильнейшая вибрация корпуса которого стала одной из причин вывода судна в 1907 г. из борьбы за скорость. На этом судне, построенном в 1900 г., были установлены самые мощные по тому времени паровые машины четырехкратного расширения, оказавшиеся не только малоэкономичными, но и источником сильнейшей структурной вибрации по всему корпусу.
В 1901 г. выходят в свет научные работы русских ученых- кораблестроителей
Ивана Бубнова (1872-1919 гг.) и Крылова по теории непотопляемости корабля, позволяющие в корабельных условиях не только использовать таблицы непотопляемости, разработанные еще Макаровым, но и производить расчетное определение посадки и остойчивости поврежденного и спрямленного судна. Использование методики Бубнова и Крылова корабельным инженером В. Костенко во время Цусимского боя в мае 1905 г. спасло броненосец “Орел” (рис.48) от гибели, тогда как три других однотипных корабля затонули в ходе сражения.
Значительным вкладом Бубнова в теорию и практику проектирования судов явилась статья "Основы статистики судостроения", опубликованная в этом же году. В этой научной работе он впервые к проблеме составления уравнения нагрузки подходит с методологических позиций, разработав методику учета весов и формирования их уравнения, что в дальнейшем будет способствовать единообразию в сборе и подготовке информации по нагрузке и значительно облегчит работу не только конструкторам, но и экипажам кораблей.
 |
Краткая биографическая справка:
Иван Григорьевич Бубнов, русский инженер - кораблестроитель и ученый, основатель современной строительной механики корабля. Окончил Петербургское Морское инженерное училище и Морскую академию, автор работ по прочности и строительной механике корабля, теории подводного плавания
и прочности подводных лодок, разработал теорию спуска судна по продольному стапелю, внес существенный вклад в развитие теории проектирования судов. Участвовал в проектировании первых русских линейных кораблей и линейных крейсеров, разработал оригинальные способы испытания подводных лодок, руководил проектированием и постройкой первых русских мореходных подводных лодок “Дельфин” и “Барс”.
|
В этом же году в России была опубликована научная статья известного корабельного инженера Николая Кутейникова (1872-1921 гг.) “Разбор элементов подводных судов”,
которая явилась одним из первых трудов, посвященных вопросам проектирования подводных лодок - анализу опыта проектирования, прогнозированию дальнейшего пути развития и определению основных тактико-технических элементов подводных лодок ближайшего будущего.
События 1901 г.
- В Германии строится самый большой чисто парусный корабль мира - 5-ти мачтовый “Пройссен”, длина стального корпуса которого составила 124,2 м, а водоизмещение 11600 т.
- Во Франции проходит мореходные испытания первая подводная лодка двухкорпусной конструкции Макса Лобефа (1864-1939 гг.) “Нарвал”(D=117/202 т) с паровой машиной для надводного хода и электромотором для подводного.
- Плавание по Арктике первого в мире арктического ледокола “Ермак” до Новой Земли и Земли Франца Иосифа.
- В США строится первая подводная лодка Джона Голланда (1840-1914 гг.) “Аддер” с четырехцилиндровым газолиновым двигателем для надводного хода и электромотором для подводного.
- По тоннажу стальные суда в 2,5 раза превосходят железные.
- В Англии построено первое гражданское судно-паротурбоход - речное пассажирское судно “Кинг Эдуард” (D=700 т, v=20,5 уз).
- Шведский геолог и исследователь Отто Норденшельд (1869-1928 гг.) возглавляет первую шведскую экспедицию на судне “Антарктик” к берегам Антарктиды, которая завершится в 1903 г. сбором обширного материала по геологии и географии этого континента (Земля Грейама).
- Поиски на шхуне “Заря” экспедицией русского полярного исследователя Эдуарда Толля (1858-1902 гг.) мифической Земли Санникова в районе Новосибирских островов.
- Трагедии американских пароходов “Сити оф Рио де Жанейро” и “Сан Рафаэль”: первый разбился о скалы на входе в бухту Золотой Рог Сан Франциско, в результате чего из 200 пассажиров удалось спасти только 81 чел. и вместе с пароходом на дно ушли золото на сумму 3 млн. долл. и опиум на сумму 1,5 млн. долл.; второй затонул в той же бухте в результате столкновения с пароходом “Саусалито” и вошел в мировую историю благодаря роману Джека Лондона “Морской волк”.
- Рейсы в Средиземном море круизных пассажирских судов - немецких пароходов “Принцесса Виктория Луиза” и “Кобра”.
Рис. 46. Английский контрминоносец "Кобра" (L= 68,1 м; B= 6,2 м; T= 2,2 м; D= 430 т; v= 36 уз; N= 12000 л.с.) вошел в историю как один из первых турбинных боевых кораблей. Вместе с тем, его трагическая судьба выявила проблему взаимодействия чрезмерно облегченного корпуса и мощной энергетической установки: в 1901 г. этот корабль на полном ходу разорвался надвое и в считанные мгновения затонул вместе с 67 членами экипажа.
В 1903 г. французский ученый И. Фредхольм формулирует метод
интегральных граничных уравнений, позволяющий решать задачи взаимодействия материальных систем с заданными граничными условиями по поверхности, что позволяет перейти к решению не только задач теории упругости однородных тел, но и взаимодействия сплошных сред с различными характеристиками.
События 1903 г.
- По проекту К. Боклевского в России построен первый в мире дизель-электроход “Вандал” (D=1150 т), на котором были установлены дизель-генераторы суммарной мощностью 360 л.с.
- Итальянский корабельный инженер Витторио Куниберти (1854-1913 гг.) высказывает идею сосредоточения на линейном корабле возможно большего числа орудий самого крупного калибра, способных нанести противнику гибельные удары в самые защищенные его части.
- Во Франции построено первое дизельное судно с прямой передачей на винт - теплоход “Пти Пьер”, на котором был установлен реверсивный дизель мощностью 25 л.с.
- В Германии для пассажирского лайнера “Кайзер Вильгельм II” создана самая мощная паровая машина четырехкратного расширения мощностью 22 тыс. л.с., которая явилась последним предсмертным достижением этого типа судового двигателя.
- В Англии построен трехвальный истребитель “Велокс” с комбинированной энергетической установкой (v=33,6 уз), где средний винт вращался паровой машиной экономичного хода, а бортовые винты - паровыми турбинами форсированного хода.
- На о. Беннета в Арктике найдены останки экспедиции Э.Толля, пропавшей без вести в 1902 г.
В 1904 г. немецкий ученый-гидромеханик Людвиг Прандтль (1875-1953 гг.)
исследует пограничный слой и выявляет зависимость коэффициента трения воды от числа Рейнольдса. В своей научной работе “О движении жидкости при очень малом трении”, изданной в 1905 г., Прандтль объясняет сопротивление формы (вихревое сопротивление) при обтекании тела жидкостью отрывом ее пограничного слоя (рис.47). Впоследствии им будет предложен очень эффективный способ ламинаризации пограничного слоя с помощью его отсоса, который, в частности, эффективно реализован на “турбопарусе", установленном сначала на экспериментальном парусном катамаране "Мулен а/ Вент" в 1983 г., а затем и судне Жака Кусто “Алсион” в 1985 г. (рис. 70).
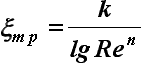 , (1904 г.)
, (1904 г.)
где xтр - коэффициент сопротивления трения гладкой пластины; k -эмпирический коэффициент; n - показатель степени логарифмической функции от числа Рейнольдса.
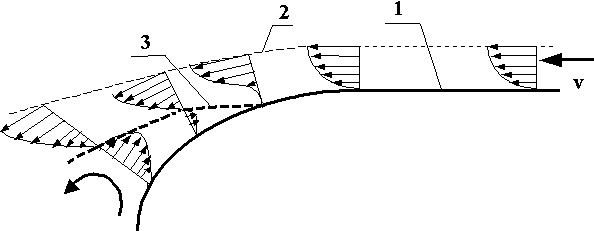
Рис.47. Пограничный слой и его отрыв в кормовой оконечности судна: 1 - ватерлиния корпуса судна; 2 - граница пограничного слоя; 3 - граница отрыва пограничного слоя.
Дальнейшее развитие теория пограничного слоя получает в трудах немецкого ученого Теодора Кармана (1881-1963 гг.), который исследует, в частности,
автоколебательные движения в воде вертикальных круговых цилиндров. Позднее своеобразный след сорванного пограничного слоя за цилиндром получит название "дорожка Кармана".
 |
Краткая биографическая справка:
Людвиг Прандтль, немецкий ученый гидраэроодинамик, один из основателей аэродинамики и научной шеолы по прикладной гидроаэромеханики, профессор. Окончил Высшее политехническое училище в Мюнхене, преподавал в Высшем техническом училище Ганновера и Гетингенском университете, директор Института аэродинамики в Гетингене. Труды по теории пограничного слоя и турбулентности, в том числе в свободной атмосфере, сверхзвуковых истечений и теплопередачи в потоке. Работы по теории упругости и пластичности, газовой динамике и динамической метеорологии. |
События 1904 г.
- Героический бой у Чемульпо крейсера “Варяг” и канонерской лодки “Кореец” с японской эскадрой и блокирование главной военно-морской базы русского Тихоокеанского флота в Порт-Артуре, означавшие начало русско-японской войны 1904 - 1905 г., в результате чего 1-я Тихоокеанская эскадра из 56 боевых единиц потеряла 37 кораблей погибшими и 5 интернированными в иностранных портах.
- Постройка русским инженером Михаилом Налетовым (1869-1938 гг.) в осажденном Порт-Артуре на собственные средства первого в мире подводного минного заградителя, который, однако, пришлось уничтожить перед сдачей базы в 1905 г., так и не применив его в боевых действиях.
- В Англии проходят испытания первые крупные морские паротурбинные суда - пассажирское судно “Куин” и крейсер “Аметист”.
- Лейтенант русского флота С. Янович впервые оснащает свою подводную лодку “Кета” устройством, обеспечивающим работу двигателя внутреннего сгорания под водой (“шнорхель”, РДП).
- Начато строительство Панамского канала, которое продлится до 1914 г.
- Подрыв флагманского броненосца “Петропавловск” на минной банке у Порт-Артура, в результате которого вместе с 640 членами экипажа погибли, находящиеся на корабле, командующий Тихоокеанским флотом С. Макаров, минный инженер К. Шульц, художник-баталист В. Верещагин, артиллерийский инженер А Мякишев.
- Норвежский инженер Бергаф предлагает способ измерения глубины дна по времени, в течение которого звук, посланный с корабля, отразится от дна и вновь возвратится на корабль (принцип эхолота).
В 1905 г. был опубликован курс лекций по проектированию судов корабельного инженера и первого декана кораблестроительного отделения Петербургского политехнического института Константина Боклевского (1862-1928 гг.), представляющий собой первую попытку формирования теории проектирования судна в виде самостоятельной научной дисциплины.
 |
Краткая биографическая справка:
Константин Боклевский, русский инженер-кораблестроитель, педагог и ученый, генерал-майор, член координационного органа при Совете министров, организатор Русского Регистра и председатель его Технического совета. Окончил кораблестроительное отделение Технического училища морского ведомства и Морскую академию, работал в Петербургском Новом Адмиралтействе помощником строителя, наблюдающим и строителем миноносцев в Одессе и Николаеве, наблюдающим за постройкой кораблей во Франции, руководил постройкой броненосца «Бородино», крейсера «Олег» и транспорта «Камчатка». С 1902 г. декан кораблестроительного отделения Петербургского политехнического института. Автор проекта усовершенствованного мореходного миноносца и автономного броненосца с дизель-электрической энергетической установкой,
трудов по корабельной архитектуре.
|

Рис.48. Новейший русский эскадренный броненосец “Орел” (L= 121 м; B= 23,2 м; T= 8,0 м; D= 13732 т;v= 17,5 уз; N=16300 л.с.) уцелел после Цусимского побоища в 1905 г. во многом благодаря таблицам непотопляемости и инструкциям по расчетному определению посадки и остойчивости поврежденного и спрямленного корабля, которые были на его борту.
События 1905 г.
- Американской шхуной “Атлантика” установлен рекорд скорости для парусных кораблей на трансатлантической линии между Нью-Йорком и Англией - 12 суток 4 часа, который был улучшен только в 1980 г. тримараном “Пан Дюик IV”.
- Французский инженер, один из пионеров авиации, Шарль Даламбер строит и успешно испытывает второй глиссер, который, в отличие от первого (1897 г.), оснащен бензиновым двигателем.
- В Италии по проекту В.Куниберти построен эскадренный броненосец “Витторио Эммануэль”, на котором впервые в судостроении применена корпусная сталь повышенного сопротивления и вторая броневая палуба, что вместе с увеличенным числом орудий главного калибра и повышенной скоростью сделало его самым лучшим кораблем этого вымирающего класса.
- Гибель 2-ой (З.Рожественский) и 3-й (Н.Небогатов) Тихоокеанских эскадр в Цусимском сражении с японским флотом адмирала Хейхатиро Того (1847-1934 гг.) во время русско-японской войны, которое явилось самым жестоким поражением русского флота за всю историю его существования и предрешило исход войны в пользу Японии: из 30 боевых кораблей эскадры уцелело 13, причем во Владивосток прорвались только три корабля.
- Революционные выступления русских матросов на броненосце “Князь Потемкин-Таврический” и крейсере “Очаков” Черноморского флота.
Глава 4. Период специализации корабельных наук ( с 1906 г. по 1945 год )



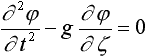 ;
;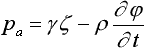 (уравнение Лагранжа); (1865 г.)
(уравнение Лагранжа); (1865 г.)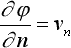 ,
,
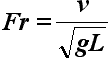 ;
; ; (1869 г.)
; (1869 г.)
 - циркуляция скорости,
м2/c; L - контур циркуляции; /dr/ = dL - направленный элемент контура; n - направление нормали к поверхности S; v - скорость,
м/с.
- циркуляция скорости,
м2/c; L - контур циркуляции; /dr/ = dL - направленный элемент контура; n - направление нормали к поверхности S; v - скорость,
м/с.

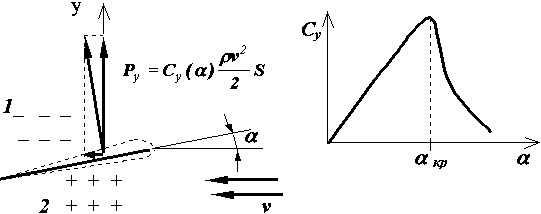


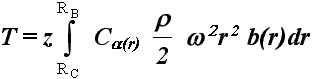 , (1878 г.)
, (1878 г.)



 ,
,
 , (1885 г.)
, (1885 г.)





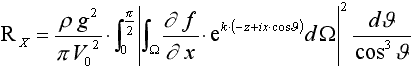 , (1898 г.)
, (1898 г.)


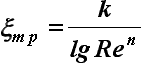 , (1904 г.)
, (1904 г.)


