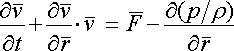 , ... ... (1)
, ... ... (1)Трехмерная тензорная математика вычислительных экспериментов в гидромеханике
Все же, что не выводится из явлений, должно называться
гипотезою, гипотезам же метафизическим, физическим,
механическим, скрытым свойствам, не место
в экспериментальной философии.
Исаак Ньютон
Современная история физико-математических наук берет свое начало от фундаментальных исследований и многочисленных опытов классической механики Исаака Ньютона, обладавшего изрядным трудолюбием и изобретательностью. Его аналитические обоснования механики, геометрический и вычислительный аппарат в форме дифференциальных разностей (флюксий), успешно используются и сегодня для решения самых разнообразных технических задач. Лондонское королевское общество и Парижская академия наук совместно создавали современный фундамент классической механики, определив главные пути эпохи научно-технических достижений, – эпохи все менее и менее полагавшейся на созидательное значение естественнонаучной философии; на древние метафизические познания в области прикладной механики и физики.
Жаль, что в наше время философия, как наука, разделилась, отчасти сокрыв глубокие интересы к познанию естественной природы, уйдя в тень эклектичных дискуссий о бытии и сознании. Веление времен всецело согласуется с житием простых людей, со взрывами социальных революций и стремительным прогрессом в освоении огромных земных пространств, получением удивительных технических знаний, ознаменовавших путь от чисто технических идей Леонардо да Винчи к теоретическим основаниям механики сплошных сред Леонарда Эйлера, к изумительному и задумчивому развитию современной научно-технической революции.
Как и всякое новейшее инструментальное средство, вычислительная математика претендует на революционное обновление своих наукоемких технологий, повсеместно наполняющих среду обитания людей новыми и почти интеллектуальными устройствами. Научно-революционное брожение со временем стабилизируется на пути планомерного и методичного освоения нового инструментария, восходящего от фундамента исторического и философского осмысления математических моделей, вычислительных экспериментов и искусственного интеллекта вездесущей микропроцессорной техники, усиленных информационной интеграцией в мировые базы инженерных знаний.
Поиск путей решения прикладных задач вычислительной гидромеханики приводит к созданию специализированных языков программирования и знакомству с основами математической лингвистики, изначально ориентированных на оптимальное проектирование и эффективную реализацию сложных программных комплексов, в том числе способных к интерактивному диалогу с инженером-исследователем.
Прямые вычислительные эксперименты в гидромеханике, изначально призванные к изучению неразрывных взаимосвязей и единства процессов и явлений природы, таким образом, вновь обрели пути обобщения базовых законов механики с позиций экспериментальной философии и в терминах гибких функциональных языков программирования, допускающих единое описание как подвижных и деформируемых корпускул, так и устаревшего вездесущего и «тончайшего эфира, проникающего во все сплошные тела и в них содержащемся» [Ньютон, 1989, стр.662], всемерно обогащая «… запас опытов, коими законы действия этого эфира были бы точно определены и доказаны».
Заметим, что прикладная математика Ньютона изначально была конечноразностной, трехмерной, и с естественной пространственно-временной постановкой прикладных задач. Исчисление флюксий Ньютона сохраняется во многих задачах современной механики, и замечательно проецируется на постановку прямых вычислительных экспериментов в гидромеханике. К сожалению, удобные для решения прямых вычислительных задач, разностные численные схемы чрезвычайно сложны для чисто аналитических исследований, и до сего дня еще не блещут каноническими определениями, не допускают сколь-нибудь универсальной постановки расчетных задач, и нередко крайне противоречиво освещаются в современной технической литературе.
Ныне физико-математические модели и вычислительные изыскания Исаака Ньютона вновь широко востребованы и возвращаются на пути практического использования и быстрого совершенствования. Новые многопроцессорные компьютеры созданы как будто бы специально для возрождения слегка «подзабытых» ньютоновских математических идей, созданных когда-то в Лондонском королевском обществе морской страны ‑ Великобритании.
Словно «добротный программист», Исаак Ньютон затвердил ключевые принципы и процедуры современной естественнонаучной философии, опубликовав законы научного поиска в области прикладной механики и вычислительной математики, обобщенные им в книге «Математические начала натуральной философии» [1947, в переводе академика, морского инженера А.Н. Крылова] ( Philosophiae naturalis principia mathematica, 1726 ).
Современное научное естествознание хронологически связано с философскими трудами Ионийской школы VII-VI вв. до н.э. Иония – район на западном побережье Малой Азии. В истории древних цивилизаций трудно устанавливать истину об уровне развития математических наук, даже если такие науки и процветали на фоне великих инженерных свершений античности. Слишком много жестоких войн, культурных революций и природных катастроф нещадно влияли на целостность исторического наследия, негативно отражаясь на преемственности инженерных и естественнонаучных знаний.
Основоположники античной греческой философии связывают свои начальные знания с научными школами процветающей Финикии ‑ мореходного государства, обладавшего колониями на всем побережье Средиземного моря, на атлантическом побережье Африки, вплоть до мыса Доброй Надежды; оставившего следы торгового присутствия и инженерного строительства на всем атлантическом побережье Европы, и в том числе ‑ на английских островах.
Это во многом объясняет переплетение многих познаний в ионийской философии, странным образом отражавшей многие законы современной физики, астрономии, географии и морской навигации, привнесенные в литературно-философские повествования из специализированных технических и естественнонаучных источников инженерного сословия Древней Азии. Письменная история не уберегла ценнейших первоисточников античных наук, не сохранилось и инженерного наследия ни Финикии, ни Лидии, ни древнего Египта.
Дошедшие до нас упоминания и редкие повествования об ионийской школе Фалеса показывают обыденность отношения людей к естественнонаучным знаниям в области географии, мореходной астрономии и навигации, в древности еще не подернутых эклектиками религиозных и политических суждений. По-видимому, в структуре малоазийских научных школ просвещенные греки довольствовались популярно-просветительскими учениями на уровне начальной подготовки инженерно-технических кадров в удаленных греческих провинциях. Может быть, по этой причине древние цитаты и пересказы отличаются упрощенным изложением физических понятий (peri physeos - учения о природе), в то же время касающихся фундаментальных основ строения микромира и космоса.
После восстания в 494 г. до н.э. полностью разрушена столица Ионии, город Милет. Многие из ученых мужей нашли пристанище в активно развивавшихся Афинах, привнеся в греческую философию остатки технических достижений малоазийских наук, и отчасти промышленных технологий и ремесел.
Фалес (625-547 гг. до н.э.) – философ и ученый, пользовавшийся непререкаемым научным авторитетом. Фалес – знатный гражданин Милета, получивший техническое и морское образование в Финикии, изучивший математические науки и мореходную астрономию в Лидии, познавший таинства египетских жрецов в длительных странствиях по Нилу.
Уровень образования и высокий общественный статус Фалеса позволял ему правильно оценивать военно-политическую ситуацию в Малой Азии и влиять на геополитические решения в жизни Милета и Ионии в целом. Фалес много времени проводил в дальних странствиях, привнося свет научных знаний во многие средиземноморские страны, активно влияя на становление общественного образования и научных школ в Греческом государстве. Античная Греция с благоговением признает Фалеса первым из семи мудрецов, своим первым просветителем и фактическим основателем будущей школы греческой философии. Ученый, философ и путешественник, Фалес стремился передать грекам свои обширные познания о мореходной астрономии, океанографии и других морских науках, отчего восхищенные греки называли его не иначе как поклонником и проповедником водной стихии. Сохранилось его любопытное гидромеханическое высказывание о происхождении вселенной: « … вода есть начало и конец всего, ибо из нее путем сгущения и испарения составляется все и все ею поддерживается, вследствие чего происходят колебания земли и вихри и движение светил, и все увлекается и течет сообразно природе первого родоначальника всего сущего».
С именем Фалеса связываются также и основополагающие математические знания: он ввел в пользование древних европейцев современный календарь и двенадцатеричную систему счисления; был автором пособия «Судоводительская астрономия», в котором излагались математические расчеты по астрономии и навигации с использованием звезд; умел рассчитывать и предсказывать солнечные и лунные затмения; правильно объяснял природу нагонных наводнений на Ниле.
Отметим еще раз: античные математические науки опирались на двенадцатеричную систему счисления, которая позволяла формализовать метафизические идеи с помощью цифр, трактуя их как в диалектическом противопоставлении фактов, так и в троичном (пространственном) объединении противоположностей.
В то же время судьба философского учения Фалеса является свидетельством безвозвратной утери практически всех достижений древне-античной цивилизации Восточного Средиземноморья, научно-философское наследие которого было рассеяно при многократных переделах земель и переменах в сознании людей в эпоху становления современных политических режимов и мировых религий.
Пифагор (570-497 гг. до н.э.). По преданию в молодости Пифагор учился в Египте, отчего в пифагорейском учении немаловажную роль играют политико-религиозные и даже мистические направления, обосновывающие идеалы «аристократии духа» во «владычестве лучших», живущих и поныне в элитарных кругах, оторванных от реальной инженерной практики. Научная методология разделяла познание на две части: «acousma» – услышанное; и «mathema» – знание.
Пифагор утверждает, что «все есть число», вводя таким образом новую логику математизации знаний. Под термином «число» трактуются «четыре канонических начала» стихий природы – «земля, вода, воздух и огонь». В случае законов Вселенной это уже квадрируется как: - «арифметика; геометрия; астрономия и музыка»; а также – «квинтэссенция» (пятая - сущность) как – «общемировой эфир».
По сути же, Пифагор декларативно вводил социальные и этические нормы, создавал экономические и политические законы управления государством. Безусловно, плодотворной была идея числовой и геометрической гармонизации мира, опиравшаяся на пятеричные законы музыкальной гармонии, по сути же – апеллировавшая к непознаваемости искусства и отвлеченно прекрасного.
Анаксагор (500-428 гг. до н.э.), являясь прямым наследником ионийской научной школы, более 30 лет жил и занимался просветительством в Афинах. В своем физико-философском учении оперирует понятиями малых элементов с однородными свойствами (семян или гомеомерий), которые всегда входят во все вещества, в совокупности определяя его внешние и внутренние свойства. Анаксагор оперирует понятиями очень близкими по смыслу современным построениям гидродинамической модели мира: вводит понятия эфира и воздуха, одновременно упоминая о корпускулярных моделях законов взаимодействия твердых тел и жидкой, деформируемой и неразрывной окружающей среды.
Ярким высказыванием Анаксагора о природе материи является следующее: « … никакая вещь не возникает и не уничтожается, но соединяется из существующих вещей и разделяется. И таким образом, правильнее было бы назвать возникновение соединением, а уничтожение – разделением … ». Вещество Анаксагор мыслит в форме непрерывных субстанций «гомеомерий» (семян), количественное преобладание которых определяет видимые и ощущаемые свойства предметов: « … следует полагать, что во всех соединениях содержится многое и разнообразное, в том числе и семена всех вещей, обладающие всевозможными формами, цветами, вкусами и запахами …». Механизм соединения и разделения веществ Анаксагор называет «абсолютным разумом». Физика Анаксагора становится более естественной, если «Разум» переопределить обобщенным понятием физических законов, относящихся к материальным телам и энергоемким континуумам, или ‑ реальным сплошным средам.
Из высказываний Анаксагора можно отметить его вовлеченность в решение инженерных и технологических проблем Древней Греции: «… Таким образом происходит вращение и отделение этих веществ под действием силы и скорости. … Остальные вещи имеют часть всего, Разум же беспределен и самодержавен и не смешан ни с одной вещью, но один он существует сам по себе. … Во всем заключается часть всего, кроме Разума, но существуют и такие вещи, в которых заключается и Разум». Последнее выражение предвосхищает средневековую гидромеханическую модель мира, основанную на замкнутых потоках энергии движения эфира в ограниченном пространстве, как процесса концентрации энергии-материи и ее независимое существование в непрерывном пространстве - времени.
Трудно сказать об истоках естественнонаучных познаний, Анаксагора, которые и через 20 столетий столь же актуальны, и столь же дискуссионны: « … – все устроил Разум, а также то вращение, которое совершают звезды, Солнце и Луна, а также отделившийся воздух и эфир. … Солнце снабжает Луну своим светом. … Радугой же мы называем отражение Солнца в облаках. … Гром и молния имеют причиной столкновение и трение облаков. … Затмения Луны происходят оттого, что ее загораживает Земля, … солнечные же затмения бывают, когда во время новолуния Луна загораживает [собой Солнце] … Небо состоит из камней и держится вследствие сильного круговращения. … Светящиеся небесные тела - суть раскаленные камни, захваченные круговращением эфира … »
Эмпедокл (484-424 гг. до н.э.) уже не мог учиться в Милетских университетах, так как за 10 лет до его рождения столица Ионии была разрушена. Эмпедокл нередко посещал италийские штаты Греции, где ознакомился с общественно-политическими и естественнонаучными учениями пифагорейцев. Но все же постижения «аристократии духа» не завели его под сени «владычества лучших». Эмпедокл известен активным образом жизни: выступлениями на олимпиадах; участием в войнах, что заметно политизировало его физико-философские работы и придало им яркую метафизическую окраску.
Эмпедокл, также как Фалес и Анаксагор развивает гидроэнергетическую идею происхождения вещества и вселенной. По его представлениями Мир был раздроблен на элементарные гомеомерии и спрессован в горячий газообразный шар, внутри которого содержалось сразу все и в равных количествах, - и в таком состоянии существовал мировой «Хаос». После нарушения устойчивости столь напряженного «Хаоса» он стал расширяться, а образовавшееся в результате расширения вращение (чем не классическая гидромеханика!) разделило вещества с разными свойствами, что и привело к многообразию нашего Мира, который может быть охарактеризован четырьмя главными состояниями первообразующих элементов: «земля», «вода», воздух» и «огонь» (огонь – эфир).
Левкипп (500~440 гг. до н.э.), а позднее Демокрит (460~370 гг. до н.э.) опирались на пифагорейские учения и развивали одно из частных направлений физики Анаксагора и Эмпедокла. Элементарные гомеомерии (семена) наделялись свойствами корпускул - атомов, между которыми постулировалась возможность существования пустоты. Дискретное упрощение свойств материи вело к частным заключениям от противного, путем утверждения главенствующих гипотез.
В античные времена учение о множественности первооснов мира становилось актуальным учением о жизнестойкости цивилизации, а философия обрела общественную значимость. Так учение Демокрита вошло в медицину, в политику, в пророчества и в бизнес. Учение Левкиппа и Демокрита показало пути синтеза разнообразных познаний природы, даже если естественнонаучные идеи не формализованы физическими законами и строгими математическими зависимостями.
Сократ (469-399 гг. до н.э.) и Платон (427-347 гг. до н.э.) создавали свое философское учение в условиях расцвета Греческой государственности.
В демократических Афинах высоко ценилось образование и научное знание, что привело к расцвету всевозможных эклектичных идей и мнений, как естественнонаучных, так и оккультных. Бесконечные дискуссии и бурные споры софистов подготовили почву для сквозной систематизации научных знаний, введению универсальной научной терминологии, сохранившейся и в современной философии всех языков мира: phisis и homos – природа и человек; thesis – установление; techne – искусство … и т.д.
Сократ, описанный Платоном, представляется проповедником научных знаний тех времен, озвучивающим методологию познания природы, в форме диалогов обосновывающим множество этических, эстетических и социально-политических установок. Диалоги Платона основаны на диалектической логике, справедливость которой ставилась в зависимости от условий существования изучаемого явления, как в пространстве окружающих событий, так и во времени.
Методология Сократа не допускала односторонних заключений, призывала к обоснованному изучению всех мнений и всех известных факторов, имеющих прямое отношение к обсуждаемой научной проблеме.
Механистические воззрения Сократа во многом опираются и развивают представление о природе Анаксагора, расширяя абстракцию беспредельного и самодержавного Разума на единого Бога, к которому сводятся не только законы природы, но также и социальные условия жизни общества; этические нормы в науке и жизни людей.
В частности, Платон определял первый этап накопления научного знания как процедуру синтеза и поиска единого начала в различных проявлениях природы, что в современной терминологии определяется как проектирование: «снизу-вверх». В высшей точке такое восхождение достигает божественных вершин, однако истинно научным оно становится только при условии непротиворечивого анализа всех результатов исследования на поверочном пути «сверху-вниз», на пути единения различных знаний о природе, ярко проявляющем истинность божественных идей в естественной природе и в жизни людей.
Учения Сократа и Платона оказали самое позитивное и миротворческое влияние на все последующее развитие философского и естественнонаучного знания. Академия Платона просуществовала более 900 лет, что позволило Эллинистической философии сохраниться в культуре и науке наших дней, неизменно освещая пути отступления из плена мистики и засилья догматизма.
Аристотель (384-322 гг. до н.э.). По-видимому, Аристотелю были доступны труды ионийских философов, и в том числе научные источники финикийцев и египтян, с которыми Греция имела постоянные научные, политические и торговые связи. Аристотелев Лицей, как независимая школа философии, уже не была ориентирована на решение чисто прикладных задач своего времени. Оставаясь чисто теоретической и умозрительной наукой, вобравшей в себя многочисленные схоластические учения античности, эта школа вела своеобразный логико-философский тренинг просвещенных граждан Греции, готовя их к самостоятельному использованию импортированных из Малой Азии инженерных технологий в строительстве, мореплавании, военных науках, торговле, государственном управлении и др.
Любопытно, что любой теоретический вопрос Аристотелем изучается параллельно и как минимум в трех независимых ипостасях, позволяя принять в качестве истины наиболее ценные для читателя обоснования. Нередко в трилектике Аристотеля сначала ставится и обосновывается какой-либо научный вопрос; затем эта же постановка вопроса полностью опровергается с целью поиска не менее обоснованных выводов, но с диалектически обратных позиций; чтобы в заключение показать полезность унификации логических противопоставлений при их практическом использовании. Поиск условий существования физического явления Аристотелем всегда превращается в отдельную и довольно сложную задачу познания природы.
Так, в трактате «О небе» Аристотель ставит вопрос о форме Земли. В первой части Земля круглая и вращается вместе с Луной вокруг Солнца. Во второй части все это уверенно опровергается, и вопрос представляется неразрешимым в принципе. Это позволяет в заключение обсудить методы примирения противоречивых доказательств, показав, что задача о форме Земли может быть решена исходя из потребностей реальной практики. Если строителю удобнее вести расчеты на плоской Земле, - то это правильно; мореплавателю для расчета географических координат и расстояний нужна сферическая Земля, - то он тоже вправе использовать астрономические законы для сферической и выпуклой Земли; а если астрологу удобнее, чтобы звезды были в центре Мироздания, - то он тоже вправе искать пророчества в геометрических фигурах, где вогнутая земная поверхность плывет внутри особого пространства.
В обоснование гидромеханической модели Мира у Аристотеля находим ключевые понятия абсолютного времени, пространства и наполняющего их неразрывного и вездесущего эфира:
1. В природе все есть движение. Локальное движение есть изменение положения тела с течением времени. Локальное движение разделяется на естественное и насильственное. Движение тела непрерывно поддерживается как парус на ветру воздухом (эфиром), стремящимся занять место, освобожденное в своем движении брошенным телом;
2. В динамике тело непрерывно находится под действием некоторой силы (энергии) и скорость его прямо пропорциональна приложенной силе и обратно пропорциональна сопротивлению среды. Отсюда следует, что в пустоте скорость стала бы бесконечно большой, и соответствующее движение приобрело бы свойство вездесущности.
Отсюда вывод: «Природа не терпит пустоты»!
Если же допустить существование пустоты, то «невозможно было бы сказать, почему тело находится в движении, должно оставаться именно тут, а не там, ибо пустота, как таковая не несет в себе никакого различия». Таким образом, Аристотель абсолютно строго высказался о необходимости существования материальной системы отсчета, что в случае гидромеханической модели мира служит фундаментальным законом соотнесения кинетической энергии относительного движения в непрерывной и деформируемой среде.
Далее Magistr dixit [1]: В пустоте нельзя выделить никакого предпочтительного движения: ни вверх, ни низа, ни правого, ни левого. Пустота пассивна и невозмутима. Следовательно, ее нет в нашем ограниченном мире.
Учение Аристотеля всегда верно, исторически это утверждение может считаться глубоко обоснованным и потому справедливым. К сожалению, это учение настолько полно и всесторонне, что играющим в науку ученикам иногда проще опираться на какое-либо из противопоставляемых Аристотелем заключений, и тем самым недооценивать (и дискредитировать) методологию Аристотелевского Лицея в познании окружающего Мира.
Лицей Аристотеля ‑ это особая академическая школа, объединившая и примирившая в рамках единой философии самые разнообразные учения античности и показавшая тем самым особую пользу фундаментальных познаний в жизни общества.
Роджер Бэкон (1214-1292) – знаменитый францисканский монах, которого признают прародителем экспериментального метода. Легенды приписывают ему изобретение пороха, оптических линз, подзорной трубы, компаса, паровой машины, самолета и т.д. Однако, образованнейший человек средневековой Европы проповедует на несколько особом языке: «Опыт может быть двояким: один посредством внешних ощущений …. Но этот опыт недостаточен для человека, потому, что он не полностью говорит о вещах телесных и ничего не говорит о духовных. Значит необходимо, чтобы ум человеческий использовал другой опыт, и вот почему святые отцы и пророки, которые первыми принесли миру знания, испытывали внутреннее озарение, а не придерживались одних лишь ощущений».
Леонардо да Винчи (1452-1519) – величайший инженер из всех, кого знает современная история науки. Сам же он соглашался с тем, что в молодости ему не посчастливилось в получении достойного образования, он не смог познать полноту Аристотелевой физики и математики, и потому заново сделал и научные открытия, и новые истолкования ранее известных физических законов. Это положило начало первой инженерной революции в физике.
Леонардо да Винчи многократно излагал свои принципы научной методологии. В некоторых случаях у него снова отмечается использование именно «гидромеханической ветви» философского учения Аристотеля, но уже без многозначных определений. Леонардо придерживался более простой и универсальной физической концепции: «Движение есть причина всего живого». Достаточно большое внимание он уделяет волновым движениям, называя их наиболее естественными движениями материи и причисляя к ним звук, свет, цвет, магнетизм, и даже мысль.
«Силой я называю духовную способность, невидимую потенцию, которая через случайное внешнее насилие вызывается движением, помещается и вливается в тела, извлекаемые и отвлекаемые от своего естественного бытия, причем она дает им активную жизнь удивительной мощности; она принуждает все созданные вещи к изменению формы и положения, стремится с яростью к желанной ей смерти и распространяется при помощи причин …».
Леонардо да Винчи преодолевает схоластическое обязательство о присутствии «Божественной Идеи» в творчестве, и формулирует правила познания мира почти с противоположных позиций: «Всякое познание начинается с чувств», поэтому «… и нужно ограничивать рассуждение опытом», а не простирать его за его пределы. «Никакое человеческое исследование не может претендовать на то, чтобы быть истинной наукой, если она не использует математических доказательств, и нет никакой уверенности там, где нельзя применить одну из математических наук»
В понимании Леонардо опыты сами по себе никогда не бывают ошибочными: «Ошибочными бывают лишь ваши суждения, если вы ожидаете от этих экспериментов такого действия, которое не будет следствием их». И поэтому: «Несправедливо жалуются люди на опыт, в величайшем гневе обвиняя его в обманчивости. Оставьте его в покое и обратите свои жалобы на ваше невежество, которое заставляет вас спешить со своими тщетными и вздорными ожиданиями таких вещей, которые не во власти опыта, и говорить, что он обманчив».
Конечно же, Леонардо да Винчи со своими великолепными опытами и изобретениями не мог сделать переворота в философии научного знания, его методология науки сильно уступала Магистру – Аристотелю. Однако после Леонардо уже никто не отваживался делать серьезных научных исследований без опоры на экспериментальные опыты; математические обоснования; и естественные наблюдения за природными явлениями.
Уильям Гильберт (1544-1603) разработал множество приборов и опытов для изучения электричества и магнетизма и заслужил титула «отца науки об электричестве». Гильберт изготовил магнит сферической формы и с его помощью исследовал свойства магнитного поля земного шара. Однако Гильберту не удалось определить природу электричества и магнетизма, и он даже пришел к выводу, что ему «не представляется совершенно абсурдным мнение Фалеса, приписывавшего магниту душу». Однако техническое развитие Европы ко времени Гильберта уже достигло того уровня, когда античные физико-философские учения пришли к серьезному противоречию с новыми физическими открытиями.
Строгие математические модели, базовые законы механики и аналитические методы изучения пространственно-временных явлений и динамических процессов, могут быть связаны с работами механиков Галилео Галилея, Рене Декарта в XVII веке и Исаака Ньютона в XVIII веке, определивших все аксиоматические правила векторных взаимодействий смежных элементов сплошной среды в абсолютных и локальных системах отсчета классической механики.
Галилео Галилей (1564–1642) успешно продолжил создание нового учения о строении мира, не преминув продолжить также и публичное развенчивание античных естественно-философских учений. Это была эпоха переосмысления и новой математической формализации всего философского наследия прошлого.
В те времена нередко использовался такой способ научной дискуссии, когда логически верное высказывание оппонента доводилось до диалектической крайности, что удается сделать только путем подмены условий проведения физического опыта, и – даже абсурдное заключение становилось противным физическим открытием.
Галилео Галилей формулирует и внедряет в практику научных исследований новую методологию, которая во многих областях естественнонаучных знаний успешно дожила до наших дней. Суть философской концепции Галилея состоит в интерпретации физического явления с целью очистки его от всех лишних или возмущающих причин. К примеру: «Книга природы» « … написана на языке математики, ее буквами служат треугольники, окружности и другие геометрические фигуры, без помощи которых человеку невозможно понять ее речь; без них – напрасно блуждание в темном лабиринте»
Методология Галилея вполне соответствует Пифагорейским квадрированным разделениям понятий; идеально подходит для целей популяризации науки; вполне применима для целенаправленного научного пересмотра и творческой (в хорошем смысле слова) компиляции чужих материалов:
1 фаза: - восприятие явления; - чувственный опыт, привлекающий наше внимание к изучению определенной частной группы явлений, но еще не дающий законов природы;
2 фаза: - аксиома или рабочая гипотеза. Центральный момент открытия, возникающий из внимательного и критического рассмотрения чувственного опыта, путем творческого процесса, сходного с интуицией художника;
3 фаза: - математическое развитие, то есть нахождение логических следствий из принятой рабочей гипотезы;
4 фаза: - опытная проверка – высший критерий всего пути открытия.
Галилео Галилей завещал, чтобы на обложке его собрания сочинений были написаны слова: «Отсюда станет понятным на бесчисленных примерах, сколь полезна математика в заключениях, касающихся того, что предлагает нам природа и насколько невозможна настоящая философия без помощи геометрии, в соответствии с истиной, провозглашенной Платоном».
Рене Декарт (1596-1650) продолжил дело математизации и геометризации физики. Декарт строго следовал гидромеханической концепции в физике, пытаясь во всем придерживаться непрерывности пространства и материальной связи между любыми взаимодействующими на расстоянии объектами. Для заполнения пустоты Декарт вводит понятие тонкой материи, которая находится в постоянном движении, что позволяет ему формально (и вполне обоснованно) определить концепцию гидродинамического притяжения между телами, окруженными вихревыми движениями тонкой материи.
Математического описания пространственного взаимодействия между непрерывными средами у Декарта еще не было, однако он хорошо владея геометрическими интерпретациями успешно применяет кинематические схемы движения «флюидов», связывая их с любыми материальными объектами. Поначалу флюиды наделялись свойствами переносчиков света, тепла и притяжения, затем, при описании магнитных взаимодействий, флюиды получили вихревые свойства и успешно сопоставлялись с реальными электрическими и магнитными наблюдениями.
Принципы познания природы Декарта сильно отличаются от научной методологии Галилея: для Декарта физика должна искать ответ на вопрос, почему происходят явления, по Галилею – исследовать, как они происходят; поиски причины – цель Декарта, описание явлений – цель Галилея.
Рене Декарт отрицает принцип абсолютного движения относительно пространства, в котором нет возможности оценить меру локального движения одного объекта относительно другого: «Если из двух человек один движется с кораблем, а второй стоит неподвижно на берегу…, то нет никакого преимущества ни в движении первого, ни в покое второго». Это означало введение единых векторных законов для описания физических объектов и кинематических процессов в абсолютной и в локальных системах отсчета, связанных с подвижными предметами и сооружениями. Немаловажными научными достижениями Декарта являются принципы относительности и правила локального исчисления движения при изучении механизмов взаимодействия тел в непрерывной материальной среде.
Исаак Ньютон (Newton Isaac, 1642 – 1727). Эпоха Ньютона характеризуется расцветом философских школ, научных открытий и величайших имен в европейской науке: Пьер Ферма (1608-1665), Блез Паскаль (1623-1662), Роберт Бойль (1627-1691), Христиан Гюйгенс [2] (1629-1695), Роберт Гук [3] (1635-1703), Готфрид Лейбниц (1646-1716), Эдмунд Галлей [4] (1656-1742), Даниил Бернулли (1700-1782) и другие ученые, объединившиеся в Лондонском королевском обществе и Парижской академии наук.
Ключевыми понятиями учения Исаака Ньютона являются термины: «Система мира», «Природы строй», «Великий океан истины». Ньютон открыто формулирует «правила умозаключений в физике» (regulae philosophandi), которым он неукоснительно следует сам и которые до сего дня являются основополагающими в экспериментальной физике:
Правило I. Не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений.
По этому поводу философы утверждают, что природа ничего не делает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим. Природа проста и не роскошествует излишними причинами вещей.
Правило II. Поэтому, поскольку возможно, должно относить одни и те же причины к того же рода проявлениям природы.
Так, например, дыханию людей и животных, падению камней в Европе и Африке, свету кухонного очага и Солнца, отражению света на Земле и на планетах.
Правило III. Такие свойства тел, которые не могут быть ни усилены, ни ослаблены и которые оказываются присущими всем телам, над которыми возможно проводить испытания, должны быть почитаемы за свойства всех тел вообще.
Свойства тел постигаются не иначе, как испытаниями; следовательно, за общие свойства надо принимать те, которые постоянно при опытах обнаруживаются и которые, как не подлежащие уменьшению, устранены быть не могут. Понятно, что в противность ряду опытов не следует измышлять на авось каких-либо бредней, не следует также уклоняться от сходственности в природе, ибо природа всегда проста и всегда сама с собой согласна.
Правило IV. В опытной физике предложения, выведенные из совершающихся явлений с помощью наведения, несмотря на возможность противных им предположений, должны быть почитаемы за верные или в точности, или приближенно, пока не обнаружатся такие явления, которыми они еще более уточнятся или же окажутся подверженными исключениям.
Так должно поступать, чтобы доводы наведения не уничтожались предположениями [5].
Универсальный закон тяготения Ньютона может быть сформулирован из третьего правила: если все тела притягиваются к Земле, море притягивается к Луне, а планеты к Солнцу, то мы можем заключить, что все тела притягиваются друг к другу.
В дискуссии с Лейбницем о флюидах Декарта Ньютон опускает чисто философский тезис о «природе не терпящей пустоты», требующем определения свойств гравитационных сил и механизма их передачи на расстояние. Эта неразрешимая и для современной механики проблема до конца жизни волновала Исаака Ньютона: «Причину этих свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю [hypotheses non fingo]. Все же что не выводится из явлений, должно называться гипотезами, гипотезам же метафизическим, физическим, механическим, скрытым свойствам не место в экспериментальной философии. В такой философии законы притяжения выводятся из явлений и обобщаются с помощью доказательства».
Ньютон не принимает плохо обоснованных гипотетических рассуждений о вихрях и флюидах, привлекавшихся в качестве переносчика энергии Декартом, а затем и Лейбницем, но и вовсе не отказывается от «… тончайшего эфира, проникающего во все тела и в них содержащегося…», завершая «Философские начала натуральной философии» следующим предложением: «Но это не может быть изложено вкратце, к тому еще нет и достаточного запаса опытов, коими законы действия этого эфира были бы точно определены и показаны». Убедительных опытов и математических обоснований для такого «эфира» не имеется и в современной науке.
Теоретические определения Ньютона задают абсолютное время и абсолютное пространство как фундаментальные метафизические понятия теоретической физики и геометрии.
« 1. Абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью. Относительное, кажущееся или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения мера продолжительности, употребляемая в обыденной жизни вместо истинного, или математического, времени, как то: час, день, месяц, год.
2. Абсолютное пространство, по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным. Относительное - есть его мера или какая-либо ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которое в обыденной жизни принимается за пространство неподвижное [6]. …
Возможно, что не существует такого равномерного движения, которым время могло измеряться с совершенной точностью. Все движения могут ускоряться или замедляться, течение же абсолютного времени [7] изменяться не может. …
Время и пространство составляют как бы вместилища самих себя и всего существующего. Во времени все располагается в смысле последовательности, в пространстве же – в смысле порядка положения. По самой своей сути это места, приписывать же местам движения нелепо. Вот эти то места и суть места абсолютные, и только перемещения из этих мест составляют абсолютные движения. …
Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения. Истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к движущемуся телу, тогда как относительное движение тела может быть и произведено, и изменено без приложения сил к этому телу» [8]
Таким образом, Исаак Ньютон создал стройную философию экспериментального изучения явлений природы и познания мира. Следуя правилам научного поиска и благодаря невероятной трудоспособности Ньютон провел огромное количество физических опытов и создал совершенную систему фундаментальных законов прикладной механики.
Очень много интереснейших явлений природы описаны в «Философских началах натуральной философии» в главах: V – «О плотности и сжатии жидкостей и о гидростатике»; VII – «О движении жидкостей и сопротивлении брошенных тел»; VIII – «О движении, распространяющемся через жидкости», которые до сих пор создают благоприятную почву для новых и новых открытий в философии, физике и прикладной механике.
Не менее значимыми научными достижениями Ньютона следует считать открытие закона линейной, относительно скорости течения, или Ньютоновой вязкости жидкостей; исследование волновых движений в упругой и вязкой среде, а также создание вычислительного аппарата прикладной математики в конечных разностях, который использовался для практического решения задач механики и обоснования новых законов природы.
При изучении вязкости Ньютон вводит своеобразную дуальность в определениях динамики малых подвижных частиц жидкости, наделяя их как корпускулярными свойствами, так и условиями сохранения исходной массы в малых контрольных континуумах, предвосхищая, тем самым, современные построения методов прямого численного моделирования в гидромеханике.
В таком численном представлении текущие координаты движущейся точки x, y, z, непрерывно изменяющиеся во времени, Ньютон называл флюентами (fluens - течение), а скорости их изменения во времени x̉, ỷ, z̉ – флюксиями (fluxio - истечение). Приращения флюент x̉·t, ỷ·t, z̉·t за малый интервал времени назывались моментами (ныне - дифференциалами). Поиск флюксий представляется как операция поэлементного добавления моментов ко всем, зависящим от времени функциям. Например:
x²+ yz = 0 → x²+ 2xx̉t +t²+yz +yz̉t + zỷt + ỷz̉t²= 0 .
Затем исключаются слагаемые, оставшиеся неизменными из исходного выражения, а результат делится на малый параметр t. Там где малый параметр не сокращается, то эти слагаемые просто отбрасываются. В итоге: 2xx̉ + yz̉ + zỷ = 0.
Решение обратной задачи, как, например, нахождение маршрута движения по заданной скорости, приводит к определению операции интегрирования.
Дифференциально-разностное исчисление флюксий не накладывает ограничений ни на класс математических функций, ни на размерность пространства, в котором ведется исследование реальных физических процессов.
Впоследствии Ньютон осуждал процедуру отбрасывания слагаемых, содержащих моменты, за ее нестрогость, говоря, что: «в математике недопустимо пренебрегать даже самыми малыми величинамии». Встав на заманчивый путь анализа бесконечно малых, он не смог определиться с физическим смыслом отбрасываемых в исчислении флюксий моментов, зато, развивая анализ дифференциальных приближений в задачах механики, Ньютон приходит к построению полиномиальных рядов, способных определять функции любой сложности, что и поныне имеет самое прямое отношение к решению прикладных вычислительных задач.
Активно развивавшееся Лейбницем [9] дифференциальное исчисление изначально сводило рассмотрение пространственных процессов к точке и потому теряло возможность построения прямых и полных вычислительных методов для моделирования континуальных явлений и процессов. Обретая значительные успехи в представлении законов аналитической механики, основанных на дифференциальных разложениях скалярных функций в разнообразных системах координат, прикладные исследования не открывают новых путей философского синтеза и единой методологии познания, завещанных античным Платоном, а лишь многократно разделяются в свободном поиске внешне противоречивых естественнонаучных решений (что Анаксагор называл уничтожением). В теоретических дискуссиях обнаруживается отторжение философии и метафизики; обособление прикладной гидромеханики от общей физики; во множестве рождаются новые разделы абстрактной математики, не опирающиеся на традиционные прикладные исследования и отрицающие классические и античные задачи натуральной философии.
При ослаблении аналитических методов, опытовое познание законов природы, будучи самым достоверным инструментом экспериментальной физики, только подтверждает свою особую практическую значимость. Прямые вычислительные эксперименты в механике сплошных сред занимают промежуточное положение между эмпирическим и аналитическим познанием естественнонаучных законов, и потому обладают особым потенциалом на пути синтеза знаний о внешне противоречивых явлениях и процессах природы.
Достоинством численных схем, основанных на обобщении исчисления флюксий Ньютона, состоит еще и в том, что они идеально соответствуют требованиям для прямого моделирования непрерывных физических процессов на современных цифровых (дискретных) ЭВМ. Однако это исчисление ныне не часто используется для получения простых и наглядных решений прикладных задач гидромеханики. Прямые вычислительные эксперименты довольно медленно совершенствуются и недостаточно полно изучаются в современных университетах.
Научная философия и мировоззрение Ньютона не позволили ему продвинуться в технических науках далее простых исследований фундаментальных законов механики, и в зрелом возрасте Ньютон сосредоточил основное внимание на философских вопросах истинно научного, исторического и религиозного знания. Возможно, это явилось следствием понимания недостаточности математических познаний тех лет для углубленного изучения вновь и вновь открывавшихся явлений и законов природы, сдерживаемых в практическом освоении несовершенством технических и вычислительных возможностей для проведения все новых и новых наблюдений и опытов с достаточным уровнем научной и технической обоснованности.
Экспериментальная физика и философское мировоззрение Ньютона вполне могут быть воссозданы в качестве новой аналитической концепции прикладных вычислительных систем для постановки и решения прикладных задач гидромеханики. Возможность сквозной интерпретации физического смысла на всех этапах применения законов и правил Ньютона, создает основу для автоматического синтеза сложных процедур и адаптивного применения функциональных возможностей искусственного интеллекта, что крайне важно в областях со сложными или переходными режимами моделируемых процессов и явлений в сплошных средах.
|
Леонард Эйлер (Euler Leonhard, 1707-1783) – математик, механик и физик. В 1724 году в Базельском университете произнес речь, посвященную сравнению философии Рене Декарта и Исаака Ньютона, и был удостоен степени магистра искусств. Первые научные работы Эйлера посвящались актуальным задачам об изохроне в сопротивляющейся среде и о траекториях, а также исследованиям о наилучшем расположении мачт на корабле. Это определило главные направления его будущих исследований в прикладной гидромеханике и в морском деле. Теоретическая гидродинамика со строгими методами решения задач механики сплошных сред, создавалась Эйлером и Бернулли
[10], определившими фундаментальные основы современной теоретической и экспериментальной гидромеханики. Эйлеру удалось в строгой математической форме определить все реакции сплошной среды под воздействием точечных векторов сил, и в том числе включить в общую систему уравнений конвективные составляющие скорости течения в ближайшей окрестности малых частиц жидкости.
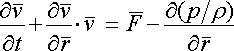 , ... ... (1)
, ... ... (1)
 F [м/с²] – кинематический вектор внешних сил;
F [м/с²] – кинематический вектор внешних сил;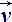 [м/с] – скорость в точке измерения течения;
[м/с] – скорость в точке измерения течения; – условное определение пространственной производной;
– условное определение пространственной производной;Скалярная запись системы уравнений гидродинамики для идеальной невязкой и несжимаемой жидкости, выполняется без привязки к каким-либо размерам элементарного жидкого континуума:
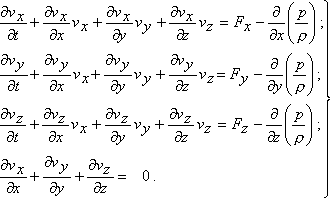 , (2)
, (2)
Эта система дифференциальных уравнений в частных производных может быть приведена к локально-сферическим координатам с помощью преобразований Громека, где кроме поступательных скоростей: vx, vy, vz будут использованы вихревые составляющие течения, пока в виде скоростей вращения элементарной частицы жидкости: ωx, ωy,ωz:
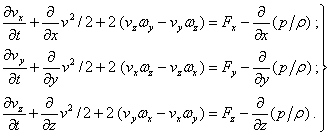 , (3)
, (3)
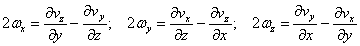 , что удобно представить в векторном виде как:
, что удобно представить в векторном виде как:
 , (3’)
, (3’)
в котором в явном виде участвуют как поступательная скорость движения, так и вращение элементарной частицы жидкости.
Полагая движение жидкости установившимся, интегрирование векторного уравнения Эйлера в форме Громека [11] приводит к закону Бернулли, справедливому вдоль линии тока в подвижной системе координат, движущейся со скоростью 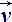 0:
0:
r·v²a/2 - r·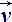 0
0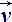 a + p = p∞, (4)
a + p = p∞, (4)
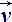 а – абсолютная скорость течения в точке измерения; р и p∞ ‑ давление в точке измерения и на удалении от источника возмущения.
а – абсолютная скорость течения в точке измерения; р и p∞ ‑ давление в точке измерения и на удалении от источника возмущения.
|
При интегрировании уравнений Эйлера (2 и 3) традиционно используется понятие поля размерного скалярного потенциала, введенного в научный оборот Эйлером в 1765 г. как: φ [м²/с], градиент которого задает вектор скорости:
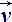 = grad φ =Ñj ,
= grad φ =Ñj ,
 , также впервые показанного Эйлером в 1767 г.
, также впервые показанного Эйлером в 1767 г.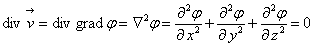 ,
,
Существование поля скалярного потенциала φ, как функционального представления поля течений жидкости, подразумевает, что векторное поле скорости является безвихревым.
Сопряженная с потенциалом функция тока [13] в трехмерном пространстве становится векторной:
 y, определяющейся с помощью нормалей к линии тока:
y, определяющейся с помощью нормалей к линии тока:
 v = Ñ ´
v = Ñ ´
 y.
y.
При моделировании поступательного потока  v∞ в качестве потенциала употребляется скалярное произведение с вектором
v∞ в качестве потенциала употребляется скалярное произведение с вектором  e [м] единичной длины, задающим направление поступательного потока в пространстве:
e [м] единичной длины, задающим направление поступательного потока в пространстве:
φ0= v∞·
v∞· e. (5)
e. (5)
Градиент этого произведения всегда сводится к вектору  v∞.
v∞.
В определении пространственного источника выражение для потенциала скорости представляется как:
φ= -Q/( 4p·r ), (6)
где: Q [м³/с] – задает объемный приток жидкости из точечного источника. Получим радиальное поле скорости течения жидкости, зависящее только от квадрата расстояния до точечного источника:|  v | = vr = -Q/( 4p·r²) (6’)
v | = vr = -Q/( 4p·r²) (6’)
 qS=
qS= q·ds
, (6’’)
q·ds
, (6’’)
 qS [м/с]) на поверхности с разрывом поля скорости течения по нормали к элементарной площадке d
qS [м/с]) на поверхности с разрывом поля скорости течения по нормали к элементарной площадке d s, что удобно использовать при искусственном моделировании условий непротекания через поверхность твердого тела. Для моделирования сжимаемой жидкости можно использовать распределенные по объему источники:
s, что удобно использовать при искусственном моделировании условий непротекания через поверхность твердого тела. Для моделирования сжимаемой жидкости можно использовать распределенные по объему источники:
 qω = d
qω = d  r³/d
t, (6’’’)
r³/d
t, (6’’’)
Потенциал для построения поля скорости от пространственного диполя получается в виде поляризованной функции четной степени:
φ= M ·  r ·
r ·  e / ( 4p·r³ ), (7)
e / ( 4p·r³ ), (7)
 e [м] определяет ориентацию центральной оси дипольного момента в пространстве.
e [м] определяет ориентацию центральной оси дипольного момента в пространстве.
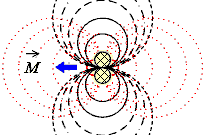
Рис. 1.1. Линии и функции тока для потенциальной модели наведенного поля скорости течения от точечного диполя.
Судя по физической размерности, поляризованные дипольные особенности должны соответствовать скорости течения жидкости, условно распределенной по объему (рис. 1.1).
Скорость течения в наведенном поле диполя уменьшается в кубической зависимости от расстояния до его центра:
 v = –
v = –  M / ( 4p·
M / ( 4p· r³ ), (7’)
r³ ), (7’)
 r³ }, которая легко моделируется алгоритмически, однако она редко употребляется в общепринятом обиходе теории поля. Наведенное диполем векторное поле наиболее наглядно (рис. 1.2) анализируется в сумме со встречным равномерным поступательным потоком жидкости:
r³ }, которая легко моделируется алгоритмически, однако она редко употребляется в общепринятом обиходе теории поля. Наведенное диполем векторное поле наиболее наглядно (рис. 1.2) анализируется в сумме со встречным равномерным поступательным потоком жидкости:
φ=  v∞·
v∞· e + M ·
e + M · r ·
r · e / ( 4p ·r³ ), (8)
e / ( 4p ·r³ ), (8)
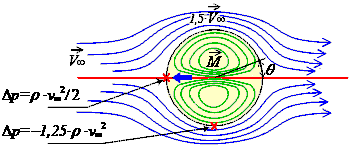
Рис. 1.2. Линии тока и основные характеристики обтекания шара, построенного с использованием модели гидродинамического потенциала.
Сам же диполь в свободном движении может перетечь в среду с совершенно иными реологическими свойствами, что отразится на его геометрических размерах и кинематических характеристиках внутренних течений, но не приведет к обновлению жидкости, изначально захваченной внутри дипольной сферы.
Бесконечность времени существования таких частиц воодушевила Кельвина [14] к предложению «вихревой модели атома», в основе которой использовано открытие Гельмгольца [15] о безусловном сохранении единожды порожденной вихревой энергии в совершенной жидкости.
Экспериментальная гидромеханика активно использовала вихревые теории для проектирования крыльев и гребных винтов, а также для обоснования вихревой природы сопротивления движению тел в вязкой жидкости - теории вихреобразования пограничного слоя, наиболее полно разработанной Прандтлем [16].
Искомый радиус сферы будет отмечен в точке на осевой линии, в которой скорость внешнего потока компенсируется встречным течением жидкости из центра диполя: r³0 = M/( 2p·v∞ ).
Объем захваченной жидкости составит: ω = 2/3·M / v∞ ).
Можно вынести величину дипольного момента из определения потенциала скорости, используя в качестве определяющего параметра только радиус сферы r0:
φ=  v∞·
v∞· r·( 1+ ½ ro³/r³ ) .
r·( 1+ ½ ro³/r³ ) .
Отсюда получаются выражения для всего поля скорости в сферической системе координат, размеченной в плоскости вектора встречного поступательного потока жидкости и просуммированного с полем течений от свободно движущегося диполя (рис. 1.2):
vr = ∂φ /∂r = v∞·cos θ ( 1 – ro³/r³ ) ;
vθ = ∂φ /∂θ = - v∞·sin θ ( 1 + ½ ro³/r³ ) . (9)
Максимальная скорость течения на поверхности сферы ровно в полтора раза превышает скорость набегающего потока.
Δ p = ρ ·v²∞ / 2 · ( 1 – 9/4 sin² θ ) . . (10)
При движении сферы различные участки ее поверхности подвержены значительным перепадам гидродинамического давления (10), изменяющемся от величины скоростного напора от Δp = ρ·v²∞ /2 в критических точках, до разрежения на поперечной окружности сферы: Δp = –1,25·ρ·v²∞ /2.
В соответствии с известным парадоксом Эйлера – Д'Аламбера, суммарная сила гидродинамического давления по всей поверхности любого тела всегда полностью скомпенсирована (рис. 1.2). Если же в потоке находится только часть сферы, например, рассеченная надвое плоской непротекаемой поверхностью, то на выступающей полусфере возникают большие суммарные отрывные усилия, возрастающие пропорционально квадрату скорости набегающего потока. Если полусфера установлена поперек потока, то превышение давления вблизи критической точки, предвосхищая парадокс Даламбера [17], не только компенсируется разрежением в расширяющемся потоке на пути к большому диаметру сферы, но и приводит к небольшому растяжению полусфер суммарным потоком с силой:
 F = –ρ·v²/2 ·
F = –ρ·v²/2 ·  Ω /8,
Ω /8,
 Ω – условно поляризованный объем сферы.
Ω – условно поляризованный объем сферы.
Кинетическая энергия для полного потока жидкости в окрестности сферы может быть получена интегрированием потенциала по ее поверхности [Павленко, 1988]:
Ke = ρ/2 ∫∫S φ ·С φ ·  n ds ,
n ds ,
 n – единичный вектор нормали к элементарной площадке ds на замкнутой поверхности Ω:
n – единичный вектор нормали к элементарной площадке ds на замкнутой поверхности Ω:
+Ke = ρv²∞/2 · 2/3 π · r³0 = ρv²∞/2 · Ω /2 . (11)
Это означает, что кроме диполя, в движении участвует дополнительный поток присоединенной массы [18] жидкости, составляющей половину объема дипольной сферы. Присоединенная масса должна учитываться во всех инерционных и энергетических зависимостях, связанных с движением любого элементарного жидкого объекта.
Особый кинематический объект – диполь, участвующий в свободном движении и состоящий из той же жидкости, что и окружающая сплошная среда, моделируется с помощью функции дипольного момента, величина которого в точности равна полному количеству движения, инициированному диполем во вне и внутри такого элементарного подвижного гидромеханического объекта:
 М=ρ·ω·
М=ρ·ω· v∞
[кг·м/с] . (12)
v∞
[кг·м/с] . (12)
|
При плоском обтекании кругового цилиндра, объем присоединенной массы становится равным объему этого цилиндра. В то же время, в отличие от пространственных тел [Войткунский,..1982], присоединенные массы эллиптического цилиндра: λ11 и λ22 , зависят только от поперечного размера, а λ66
‑ для осевого вращения эллиптического цилиндра связаны с геометрической суммой полуосей эллипсоида:
λ11= ρ ·π ·rx²; λ22 = ρ ·π ·ry²; λ66 = ρ ·π ·( rx²+ry²)² / 8 . (13)
Если положить одну из осей rx или ry равными нулю, то формулы (13) дадут присоединенные массы для обтекания и вращения плоской пластины, не имеющей собственного объема или инерции. Это еще раз указывает на особенности кинематики внешнего воздействия на неразрывную среду, в гидромеханике которой превалирует обобщенная величина возмущаемого потока, в то время как собственно форма возмущающего тела или иного источника – вторичны.
Моделирование плоских течений выполняется в рамках теории функций комплексного переменного, в полной мере реализующей двумерные аналоги трехмерных тензорных операций. Плоские модели позволяют независимо исследовать поверхностные гидродинамические особенности (распределенные и дискретные вихреисточники и диполи), моделирующие обтекание плоских контуров с помощью простых и двойных слоев. В трехмерных задачах все процессы взаимодействия элементарных частиц жидкости являются смешанными, и нередко предстают взаимопереходящими между смежными расчетными ячейками на последовательных этапах гидродинамических вычислительных экспериментов.
Плоские комплексные функции представляются в качестве векторов и тензоров, геометрические свойства которых наглядно иллюстрируются с помощью формулы Эйлера:
r = x+iy = | r |·(cos J + i·sin J ) = r·e i·J,
где: r² = x²+ y², J - угол ориентации вектора r в связной системе координат.По формуле Эйлера наглядно показывается, что произведение двух векторов в комплексной плоскости сводится к умножению их модулей и сумме угловых аргументов:
r1·r2= |r1|·|r2|·e i(J1+J2).
В двумерном пространстве функция тока доопределяет мнимую часть комплексного потенциала скорости:
W( z ) = φ + i·ψ ; d W / d z = u + i·v ,
представляющегося в качестве плоского аналога к изучаемому в этой книге тензорному представлению трехмерных течений.  M = π·r²·
M = π·r²· V∞ =
V∞ =  V∞·S – плоский диполь;
V∞·S – плоский диполь;
 G = Q + i·Г = 2π·
G = Q + i·Г = 2π· r ·
r ·  V∞ – плоский вихреисточник.
V∞ – плоский вихреисточник.
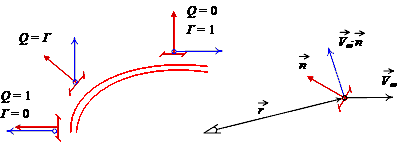
Рис. 1.3. Вихреисточники, моделирующие обтекание плоской фигуры.
Q - интенсивность распределенных по контуру тела источников;
Г - интенсивность присоединенных вихрей;
 V∞ - скорость набегающего потока;
V∞ - скорость набегающего потока;
 n - вектор нормали и длины элементарного участка контура;
n - вектор нормали и длины элементарного участка контура;
 r - расчетный радиус из точки измерения наведенной скорости.
r - расчетный радиус из точки измерения наведенной скорости.
При моделировании обтекания плоского тела с использованием суперпозиции поступательного потока и слоя вихреисточников, в комплексной плоскости (рис. 1.3) наглядно представляются свойства перераспределения интенсивностей вдоль обтекаемого контура тела.
По поверхности плоского тела должны быть распределены гидродинамические особенности в виде диполей, вызванные скорости от которых определяются как:
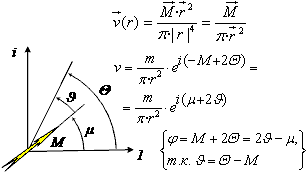
Рис. 1.4. Диполь в плоскости комплексного переменного.
r – геодезическое (кратчайшее по времени действия) расстояние от центра энергетического источника до точки воздействия;
Θ - угол для r в абсолютной системе координат;
J - угол для r в относительной системе координат, связанной с диполем;
φ - ориентация результирующего вектора вызванной скорости  v;
v;
μ - ориентации диполя  М в абсолютной системе координат.
М в абсолютной системе координат.
Скорость  v определяется в дуальном базисе (рис. 1.4) по отношению к базису, в котором определен дипольный момент
v определяется в дуальном базисе (рис. 1.4) по отношению к базису, в котором определен дипольный момент  М.
М.
Полное моделирование обтекания плоского тела может быть однозначно представлено с помощью суммы двух интегралов:
1 ‑ от равномерно распределенных по всей поверхности плоского тела диполей:  vs = ∫
vs = ∫  m / ( π·
m / ( π· r²) d S , где:
r²) d S , где:  m =
m =  vi – распределенные диполи;
vi – распределенные диполи;
2 ‑ от вихреисточников, образующих простой слой по граничному контуру плоского тела:  vL = ∫
vL = ∫  g / (
π·
g / (
π· r ) d | L | ; g=i·
r ) d | L | ; g=i· m /
m /
 L
– вихреисточники.
L
– вихреисточники.
Приведенные интегралы дают верные результаты численных расчетов для наведенного вокруг подвижного контура поля скорости при условии, что кривизной элементарного сегмента контура можно пренебречь. На сломах вблизи углов должны располагаться вихреисточники в качестве полноценных гидродинамических особенностей:
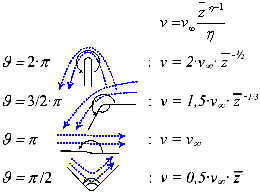
По аналогии можно расширить использование степенных функций:
– для точечного вихря: J = ∞ → v = G · z-1 / 2π ;
– для диполя: J = –π → v = 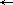 M · z-2 / π ;
M · z-2 / π ;
В математической модели плоских трохоидальных волн существует потенциал Лапласа для всего поля течения, и, одновременно, в лагранжевом представлении траекторий малых континуумов обнаруживается реальное вихревое поле для крутого морского волнения:
hw( x,z ) = A·e-kz+iσx = e-2π ( z / τ - x / λ ) ;
Vr = σ·rw ; rw = A·e-kz = e-2π·z / τ ; k·λ=2π ; σ·τ =2π ,
Решение для волн Герстнера [19] получено в 1802 году, и представляется как удивительное и поныне неоцененное открытие универсальности лагранже-эйлеровых свойств элементарных частиц жидкости, повсеместно используемых в инженерной гидромеханике.
В историческом обзоре классических моделей механики сплошных сред нельзя не упомянуть о Российской школе аэрогидромеханики Н.Е. Жуковского [20] [1949], приведшей в 1936 году к постановке проблемы «Обобщения основных уравнений аэродинамики и электродинамики», озвученной в виде предварительного научного сообщения Н.П. Кастериным [21]. В теории Кастерина рассмотрен вопрос ограниченности уравнений Эйлера и Максвелла [22] для описания реальных физических полей. Частичное расширение этих линейных уравнений с помощью вихревых теорем Гельмгольца до второго порядка, приводило к унифицированным моделям математической теории поля для задач гидродинамики и электродинамики. Однако, как будет показано в главе III в тензорных функциях, любое уточнение с повышением порядка дифференциальных уравнений гидромеханики нередко приводит к их переопределенности, чрезмерному усложнению или ‑ к формальному вырождению базисных числовых объектов.
Вкратце коснемся современных основ и перспектив развития математических моделей механики жидкости, изначально ориентированных на трехмерность пространства и минимум арифметических операций с базовыми расчетными объектами, которые по мере совершенствования архитектуры ЭВМ смогут образовать массивы активных смежных элементов памяти, одномоментно взаимодействующих на принципах гибридных аналоговых процессов с глубоко распараллеленными цифровыми потоками числовых операции.
Исторически вычислительные эксперименты в гидромеханике связаны к классической дисциплиной: «Математическая физика», ныне получившей совершенный аппаратно-технический инструментарий в виде мощных вычислителей – цифровых однопроцессорных компьютеров.
Постановка расчетной задачи с помощью разностной аппроксимации традиционных систем дифференциальных уравнений в частных производных, позволяет качественно проверить вычислительные эксперименты в гидромеханике, сопоставляя результаты как с известными аналитическими решениями, так и с натурными экспериментами для аналогичных модельных течений.
Цифровая вычислительная техника (в отличие от аналоговой) не позволяет в точности моделировать задачи гидромеханики, так как континуальные явления подменяются ограниченными по объему цифровыми массивами, а непрерывные процессы – простым и многократным последовательным перебором разрозненных параметров пространственных полей, к которым применяются только операции сложения и умножения, и всегда для одних и тех же смежных числовых объектов.
Постановка алгоритмических задач на однопроцессорных компьютерах также значительно снижает потенциальную эффективность вычислительных моделей гидромеханики, так как все описатели пространственных полей постоянно доставляются на одно-единственное универсальное арифметико-логическое устройство, где реализуются те же операции сложения и умножения, с последующим возвратом результатов в отдаленную память ЭВМ. Столь своеобразное сведение моделируемых процессов к последовательной обработке перебором больших числовых массивов, в принципе, согласуется с технологией использования только одного арифметико-логического устройства ЭВМ.
Числовые операции с существенно отличающимися числовыми величинами, к которым, например, относятся пространственные проекции в абсолютной и в локальных системах отсчета, и особенно, если в основе математической модели лежат интегро-дифференциальные аппроксимирующие разности предельно малой величины, то вычислительные эксперименты теряют разрешимость по чисто техническим причинам.
И все же, интерактивные возможности по контролю и управлению современной вычислительной техникой, ее фантастическая результативность в числовых расчетах, позволяют на новом техническом уровне всесторонне изучить существующие подходы к решению прикладных задач гидромеханики, провести комплексный анализ и экспериментальные поверки методов тензорного представления задач теории поля в классической гидромеханике; сравнить их с хорошо опробованными математическими моделями, с аналитическими и асимптотическими решениями.
В традиционной математической физике [Тихонов, 1966] рассматриваются три основных типа систем дифференциальных уравнений в частных производных, используемых при решении прикладных задач механики сплошных сред. В данном случае это дифференциальные уравнения движения, имеющие второй порядок и определяющие полное решение задач механики. В канонической форме такие уравнения становятся похожими на обыкновенные дифференциальные уравнения второго порядка, определяющие свойства их аналитических решений и дающие им соответствующие названия, как эллиптические, параболические и гиперболические.
а11· Фxx + 2·а12· Фxy + а22· Фyy + С ( x,y,Ф,ФX,ФУ ) = 0
общий интеграл этого обыкновенного дифференциального уравнения второго порядка представляется в виде следующего характеристического уравнения:а11·dy² + 2·а12·dx·dy + а22·dx² = 0.
Класс уравнения определяется знаком детерминанта этого обобщенного интеграла второго порядка, получаемого после двойного дифференцирования по одной из переменных:
a11 · d²y/dx + 2·a12·dy/dx + a22 = 0 ,
отчасти условно воспринимаемого затем, как решение обыкновенного квадратного уравнения:D = a²12 - a11 · a22.
Если:Кратко рассмотрим свойства этих классов дифференциальных уравнений в частных производных, приведенных к каноническому виду в применении к простейшим двумерным задачам, так как в трехмерных задачах такие канонические интерпретации, как правило, являются смешанными и потому существенно более сложными для какой бы то ни было интерпретации.
1) Фxx + Фyy + к·Ф + С = 0. Система дифференциальных уравнений в частных производных эллиптического типа описывает кинематику «идеальной» жидкости и чаще всего применяется к решению задач о течениях невязкой и несжимаемой жидкости. В этом классе уравнений известны аналитические (и численные) решения только для установившихся течений жидкости, получаемые исключительно с помощью неявных численных схем. Характерной особенностью численных расчетов таких течений является то, что любое изменение условий течения, пусть даже в одной из удаленных точек, требует пересчета всего массива данных, определяющего поле течения. Данный класс численных решений до настоящего времени не имеет сколь-нибудь простых и эффективных численных реализаций, особенно, если к уравнениям добавляются вязкостные поправки (параболичность), или делаются попытки построить модели нестационарных течений (гиперболичность).
Несмотря на то, что системы дифференциальных уравнений эллиптического типа определяют только стационарные течения, и не дают возможности для изучения процессов трансформации или зарождения гидромеханических процессов, их использование относится к наиболее сложному типу физических задач, как в плане их аналитического решения, так и при их асимптотическом упрощении или прямом численном моделировании. Однако именно этот класс уравнений в полной мере определяет законы классической гидродинамики, со всеми их красивыми явлениями и поразительными для теоретической механики парадоксами. Отметим, что реализация решений для течения идеальной жидкости вполне допускает бесконечные напряжения в локальных областях со сложными граничными условиями, что не может реализоваться на практике с реальными жидкостями, всегда обладающими как вязкостью, так и сжимаемостью.
Важнейшим свойством динамики идеальной жидкости является принцип прямолинейности взаимодействия удаленных друг от друга частиц жидкости, при соблюдении закона об изменении интенсивности такого взаимодействия обратно пропорционально квадрату расстояния между ними. Это важнейшее свойство ближнего взаимодействия (т.е. в пределах допустимости линейных аппроксимаций численных решений), далее будет использовано при построении обобщающей тензорной теории для реализации вычислительных экспериментов гидромеханики реальной жидкости.
2) Фxx + к·Фy + С = 0. Система дифференциальных уравнений в частных производных параболического типа описывает процессы типа диффузии или распространения тепловой энергии, где скорость процесса зависит от интенсивности распределенных полей. Это класс наиболее простых динамических уравнений, для которых хорошо отработаны вычислительные задачи в применении к нестационарным процессам, в том числе протекающим в сплошных средах с анизотропными свойствами. Однако и для параболических уравнений обычно не получается наглядных и явных вычислительных схем (даже в одномерных случаях), но зато и не возникает непреодолимых трудностей с вычислительной устойчивостью или аппроксимационной гладкостью пространственных решений.
3) Фxy + к·Ф + С = 0 или Фxx - Фyy + к·Ф + С = 0. Системы дифференциальных уравнений в частных производных гиперболического типа обычно описывают процессы в упругих средах. Пожалуй, это наиболее изученные в современной физике явления и гидродинамические процессы, освоенные и широко используемые во многих технических приложениях, связанных с излучением и регистрацией различных нестационарных и волновых процессов, в которых жидкая среда не принимает сколь-нибудь активного участия и практически не изменяет ни своих динамических, ни даже кинематических параметров (при попытке включить в моделирование собственно течение жидкости или его конвективные составляющие, математическая модель немедленно становится полной, а ее представление в рамках гиперболических численных схем - неразрешимым).
Благодаря математической простоте и сопутствующей наглядности, свойства волновых процессов наиболее изучены, они легко аппроксимируются как в прямых вычислительных экспериментах, так и в замысловатых аналитических обобщениях.
В отличие от сугубо непериодических явлений чистой гидромеханики, существование волновых процессов легко обнаруживается в самых различных природных и идеальных условиях. Множество технических достижений основывается на слабоэнергетических волновых явлениях, в которых интенсивность динамических процессов не оказывает воздействия на сплошную среду и в то же время их своеобразное постоянство, позволяет применять квазистационарный аналитический инструментарий.
Это всевозможные световые, электромагнитные и акустические волны, трансформирующиеся на механических и электромагнитных резонаторах и преобразователях. Именно для таких слабоэнергетических процессов найдено множество эмпирических решений и строгих математических соотношений, которые во многих естественных науках превратились почти что в аксиомы. К примеру, принцип Гюйгенса или волновые законы рефракции, интерференции, дифракции и т.п., которые широко анализируются с помощью множества наглядных аналогий, в основном опирающихся на одномерные математические аналитики.
В то же время, зарождение и трансформация волновых процессов выходит за рамки «стационарных» волновых моделей. В этом случае к стандартным моделям добавляются эвристики о групповой структуре волновых пакетов или дисперсионные эмпирики для учета взаимодействия с окружающей средой. Если энергетика локальных волновых воздействий превышает некоторые критические условия существования окружающей среды, то высокочастотные волновые процессы обретают признаки дуальности с корпускулами аналитической механики, а в волнах длинных – снова с чистой гидромеханикой.
Для гиперболических систем уравнений имеется множество теоретических решений и эмпирических зависимостей, - это уравнения, которые легко выводятся из простых предпосылок о динамике взаимодействия между расчетными частицами жидкости, заданными на обычных ячейках сеточной области. Такой способ построения вычислительных решений в гидромеханике наиболее близок к классическому определению «Метода конечного объема».
Методы анализа волновых сигналов хорошо отработаны и давно используются в морской технике, эти же методы легко адаптируются для прямого моделирования длинноволновых процессов в океане и в его прибрежной зоне. В последнем случае, с использованием параметризации уравнений движения и неразрывности, гиперболические уравнения в потенциалах преобразуются в традиционную явную систему дифференциальных уравнений в частных производных, определяемую через векторное поле скорости и скалярную функцию изменений уровня моря. На этих уравнениях сама природа призывает отрабатывать разнообразие методов вычислительной гидромеханики (наглядно иллюстрируя пределы применимости гиперболических аппроксимаций, проявляющих нелинейные и дисперсионные особенности распространения волн над круто меняющимся рельефом морского дна).
В частности, возможность предвычисления скорости движения волновых пакетов, зависящих от реологических свойств жидкой среды, позволяет выполнять геометрический анализ условий распространения волновой энергии с помощью быстро рассчитываемых картин волновых лучей и фронтов. Технические решения для волновой томографии, в акустических приближениях строятся с использованием разделения сигналов во времени, позволяя фиксировать параметры фронтальных и протяженных сигналов, с выделением амплитудно-частотных характеристик реверберации в сплошной среде и отраженных от препятствий опорных импульсов эха.
И все же, всякое разделение и упрощение физических зависимостей приводит к частичному сокрытию физической сущности рассматриваемых явлений, и значительно усложняет логику практического применения законов движения при решении прикладных задач механики. На основе уравнений Эйлера получены самые разнообразные решения в области прикладной гидродинамики, однако все они носят частный характер с очень ограниченной областью применимости. С помощью этих же уравнений поставлено множество других неразрешимых теоретических задач механики сплошных сред, что любому исследователю предоставляет широчайший горизонт для поиска новых физических законов и математических решений в гидромеханике реальных жидкостей.
Прямое решение уравнений Эйлера с использованием разностных разложений дифференциальных уравнений движения в частных производных (по Анаксагору это приводит к выхолащиванию исходной физической сути), обычно делается при допущениях об особых свойствах пространственных систем отсчета. В подходе Эйлера пространственная система координат считается неподвижной, что приводит к поступательным и конвективным полям скоростей и ускорений в жидкости, движущейся через инородную и жесткую расчетную сетку. В подходе Лагранжа рассматриваются поступательные движения отдельно взятых частиц жидкости, определяемых в рамках аналитической динамики свободных корпускул, что на практике сводится к неявным схемам анализа виртуальных движений для множества пространственных точек, и – к потребности в неоправданно огромных вычислительных ресурсах для работы с гигантскими и плохообусловленными матрицами.
Идея комплексного решения поставленной задачи состоит в связывании с каждой из частиц собственного локального базиса, внутри которого крупные частицы жидкости могут деформироваться и даже образовывать внутренние замкнутые течения жидкости. Соответствующие методы решения прикладных задач гидромеханики опираются на интерпретацию свойств течения по Эйлеру и по Лагранжу совместно и в качестве единого процесса, лишь условно разделяемого по этапам проведения вычислительного эксперимента на алгоритмическом уровне. К таким методам относятся методы «Маркеров и ячеек», «Крупных частиц жидкости» и другие прямые построения численных моделей в разностях, которые в последнее время стали объединять единым термином, как «Метод конечного объема». Идеология и техническая реализация такого обобщенного подхода наталкивается как на серьезные математические трудности, так и на трудности при реализации конкретного программного обеспечения ЭВМ для проведения реальных прикладных вычислительных экспериментов.
Мир компьютерных моделей не совсем однозначно отображается на современную аналитическую математику, представляющую законы движения жидкости в форме систем дифференциальных уравнений в частных производных. Нельзя ли конечноразностные объекты и операции, присущие цифровым ЭВМ, использовать как независимый и вполне самостоятельный математический инструмент прикладной гидромеханики?
Наиболее яркой публикацией о методах вычислительной гидромеханики явилась изданная в 1982 году книга О.М. Белоцерковского и Ю.М. Давыдова «Метод крупных частиц в газовой динамике», содержащей наиболее выразительное и точное описание вычислительных экспериментов в гидромеханике с использованием Лагранже-Эйлеровых подходов. В этой же книге выполнен анализ и обоснование физической сути дифференциальных приближений, которые используются в вычислительных моделях гидромеханики при замене классических дифференциальных уравнений в частных производных их конечно-разностными аппроксимациями.
В 1990 году вышел двухтомник Д. Андерсона, Дж. Таннехилла и Р. Плетчера «Вычислительная гидромеханика и теплообмен», в которой были обобщены и систематизированы многие вычислительные модели прикладной гидромеханики. В этой книге закрепился примиряющий термин: «Метод конечного объема», который также определяет технологии, достаточно близкие по смыслу к тензорным построениям вычислительных экспериментов, но, к сожалению, это справедливо только в отношении к постановочной части приводимых в двухтомнике гидромеханических задач, так как в целом в «методе конечного объема» главное внимание уделяется разностным аппроксимациям традиционных систем дифференциальных уравнений в частных производных.
Поэтому, в основе настоящей работы справедливее признать основные идеи и вычислительные технологии метода «Крупных частиц жидкости», тем более, что тензорные формализации уравнений аэрогидромеханики впервые отрабатывались и проверялись с помощью свертывания к тензорной форме больших систем разностных уравнений именно этого метода [1982].
Пионерскими исследованиями в изучаемом направлении считаются вычислительные эксперименты в аэрогидромеханике Лос-Аламосской лаборатории (США), открывшими новое научное направление по использованию свободных лагранжевых частиц для моделирования сложных течений и опубликованных Харлоу в 1955 году под определением: PIC (Particle in Cell) – метода частиц в ячейках. Метод PIC изначально был ориентирован на использование огромных вычислительных ресурсов, так как уравнения гидромеханики в форме Лагранже сводятся к неявным расчетным схемам, решаемым с использованием матричной алгебры для согласования неопределенных параметров движения и внутреннего состояния для каждой из условно свободных корпускул в потоке жидкости. Таких точечных частиц должно быть достаточно много в каждой из анализируемых расчетных ячеек, в том числе и в зонах течения с сильными разрежениями, что и обусловливало потребность в огромных суперкомпьютерных ресурсах.
Другой подход к пристальному изучению вычислительных экспериментов обусловлен признанием того факта, что аппроксимационные свойства конечных разностей представляют из себя нечто сильно отличающееся от исходной математической модели в виде систем дифференциальных уравнений в частных производных. Проработка обратных дифференциальных приближений также аккуратно выполнена Ю.М. Давыдовым [1981] с целью обоснования корректности постановки гидродинамической задачи, точности ее пространственных аппроксимаций, выявления схемной вязкости и устойчивости метода «Крупных частиц жидкости». Им было показано присутствие схемной вязкости в линейных разностных аппроксимациях, в точности соответствующей физическим свойствам ньютоновой вязкости у реальных жидкостей, величина которой связана с шагом пространственной сетки, и отчасти с расчетным шагом во времени.
Важным следствием анализа дифференциальных приближений для разностных схем вычислительной гидромеханики, стало признание факта невозможности качественного улучшения точности расчетов с помощью повышения порядка разностных схем. А именно, в схемах второго порядка формально блокируются эффекты схемной вязкости, и одновременно усиливаются искусственные добавки более высокого ‑ третьего порядка, от которых аппроксимирующие функции становятся осциллирующими, и сильно возбуждаются в зонах течения жидкости с большими градиентами.
Устойчивость в задачах гидромеханики оценивается как возможность существования интеграла для дифференциального уравнения второго порядка по скалярному аргументу - времени, получающегося в Лагранже-Эйлеровом подходе в результате двух последовательных этапов интегрирования уравнений движения первого порядка. Обычно, для достижения устойчивости численного моделирования, достаточно выбора такого расчетного шага по времени, чтобы элементарные частицы жидкости и смежные с ними ячейки не изменяли характера деформации и режима движения жидкости в течение одного расчетного этапа.
В результате были получены обоснования области применимости численных методов для традиционных математических моделей гидромеханики на неподвижных (и равномерных) Эйлеровых сетках, и что более важно, изучены критерии существования и устойчивости вычислительных процессов, выявлены математические модели, непригодные для их реализации с использованием цифровых ЭВМ.
Как и ожидалось, вычислительная математика и гидромеханика явили новое воплощение гармонии в природе, совместный Лагранжев и Эйлеров подход для непосредственного и прямого моделирования большого класса законов гидромеханики и явлений природы, «не терпящей пустоты». Это воссоздало целостное представление о физике моделируемых гидродинамических процессов, на этот раз с помощью прямых численных методов на дискретных сеточных аппроксимациях современных цифровых ЭВМ.
А именно, численные схемы метода крупных частиц (конечного объема), возродили средневековые представления Исаака Ньютона о дуальности свойств жидкости, использованные им и Робертом Гуком при определении вязких и упругих свойств реальной жидкости более трехсот лет назад.
Используемое для представления вычислительной модели тензорное исчисление традиционно применяется в гидромеханике с целью анализа состояния малых континуумов жидкости. В «Механике деформируемых сред» Арнольда Зоммерфельда [1954] довольно полно определены свойства тензоров деформации, конвективных скоростей и вязких напряжений в жидкости. В книге итальянских ученых Дж. Астариты и Дж. Маруччи [1978] «Основы гидромеханики неньютоновских жидкостей» сводятся воедино существенно различные тензорные представления, накопившиеся в гидромеханике, теории упругости и других разделах механики сплошных сред.
Тензорное исчисление [Мак-Коннел, 1963, Сокольников, 1971], являясь пространственным расширением конечно-разностной формы ньютоновских дифференциалов стало своеобразным упрощением формы записи традиционных численных схем для решения прикладных задач механики сплошных сред.
В «Прикладной механике сплошных сред» под редакцией В.В. Селиванова [1998], тензорное исчисление активно используется для анализа численных моделей Лагранже-Эйлерова подхода в аэрогидродинамических вычислительных экспериментах.
В настоящей работе не ставилось целей существенно более глубокого изучения тензорного анализа в задачах гидромеханики в целом. Активно используется только та часть тензорной математики, которая необходима для представления численных схем, числовых объектов и ключевых операций в прямых вычислительных экспериментах классической гидромеханики.
Конкретизация задачи в сторону изучения чисто кинематических процессов в динамике реальной жидкости необходима для достижения сквозной физической интерпретации всех вычислительных объектов и операций, достаточной для повсеместного контроля и своевременного применения гибридных подмен или эмпирических уточнений в подобластях с явно вырождающимися критериями моделирования.
|
Скалярные величины – числа, могут быть расширительно интерпретированы в качестве направленных в строго определенную сторону отрезков (рис. 1.5) на одномерной геометрической оси Х, начальный отсчет на которой может быть назван условно абсолютным нулем – 0. Такое представление скаляров всегда присутствует при описании проекций на базисные оси координат для векторных и тензорных величин.

Рис. 1.5. Условная отметка скалярных величин на одномерной оси координат.
Масштаб одномерных величин определяется особыми единичными векторами – ортами, отмечаемыми на координатной оси значениями ± 1. Это приводит к Ньютоновскому определению числа, как «отношения длины любого отрезка к отрезку, принятому за единицу» [Математика, 2003, с.732] (во сколько раз проекция векторного отрезка отлична от единичного орта). На такой скалярной оси может быть поставлена особая метка ‑
1. Это приводит к Ньютоновскому определению числа, как «отношения длины любого отрезка к отрезку, принятому за единицу» [Математика, 2003, с.732] (во сколько раз проекция векторного отрезка отлична от единичного орта). На такой скалярной оси может быть поставлена особая метка ‑  R’ , которая будет служить смещенным основанием для новой (локальной) системы отсчета.
R’ , которая будет служить смещенным основанием для новой (локальной) системы отсчета.
Абсолютные (условно длинные) отсчеты от общего нуля на скалярной оси будем обозначать прописными буквами –
 А, а локальные (короткие), отмеренные от смещенной метки ‑
А, а локальные (короткие), отмеренные от смещенной метки ‑
 R’, строчными буквами –
R’, строчными буквами –  а.
а.
Для перевода скалярной величины из локальной системы отсчета –  R’ в абсолютную –
R’ в абсолютную –  Х, необходимо сложить локальную длину отрезка –
Х, необходимо сложить локальную длину отрезка –  а, с величиной начального отсчета смещенной (относительной) метки ‑
а, с величиной начального отсчета смещенной (относительной) метки ‑  R’:
R’:
 А =
А =  R’ +
R’ +  a.
a.
Все слагаемые величины должны иметь одинаковые физические размерности. Операция умножения (кратности) с величиной  а возможна только в случае использования безразмерного параметра, который влияет на изменение длины (деформацию) этого локального вектора –
а возможна только в случае использования безразмерного параметра, который влияет на изменение длины (деформацию) этого локального вектора –  а. Далее, в векторном исчислении будет показано, что в операциях умножения могут участвовать размерные физические величины, но только если их компоненты измерены в связном (дуальном) координатном базисе.
а. Далее, в векторном исчислении будет показано, что в операциях умножения могут участвовать размерные физические величины, но только если их компоненты измерены в связном (дуальном) координатном базисе.
Для одномерных, «условно векторных» величин нет необходимости вводить особые правила для координатных преобразований, достаточно использования простых масштабных множителей, связанных с пропорциональными (линейными) пересчетами в окрестности точки  R’. Это означает, что величины локальных и абсолютных координатных отсчетов с точностью до произвольного безразмерного множителя могут считаться приведенными к единой координатной системе.
R’. Это означает, что величины локальных и абсолютных координатных отсчетов с точностью до произвольного безразмерного множителя могут считаться приведенными к единой координатной системе.
|
В отличие от одномерного случая, локальный базис в пространстве, также как и все векторные величины, характеризуется не только масштабными множителями относительно единичных ортов (модулями), но и ориентацией (направлением) в пространстве его координатных осей.
Формальные описания и математические действия с векторными объектами в трехмерном пространстве уже не требуют искусственных условностей.
В качестве абсолютной системы координат выбирается симплекс координатных осей, соответствующий размерности используемого пространства, при этом все базисные оси должны быть взаимно перпендикулярны (ортогональны), иметь одинаковые физические размерности и равные единичные меры (ортонормированы). Удовлетворяющие таким требованиям системы координат называют ортогональными и ортонормированными или – декартовыми. В декартовой системе координат векторные величины единственным образом представляются в виде совокупности числовых величин, образованных проекциями на координатные направления (рис. 1.6).
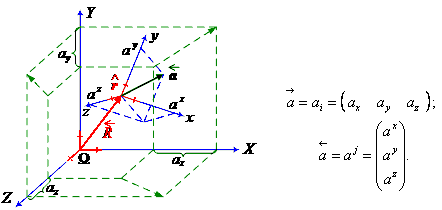
Рис. 1.6. Ковариантные ai и контравариантные a j компоненты вектора. Геометрическое и матричное представление числового объекта в проекциях глобальной и связанной систем координат.
На рисунке 1.6 показан трехмерный базис декартовой системы координат, представленный в виде простейшего (необходимого и достаточного) симплекса координатных осей, в котором любой вектор { R } единственным образом представляется в виде координатных проекций на ортогональные оси {Xi, Yj, Zk }, масштаб величин которых определяется мерой единичных векторов – ортов.
R } единственным образом представляется в виде координатных проекций на ортогональные оси {Xi, Yj, Zk }, масштаб величин которых определяется мерой единичных векторов – ортов.
Местная система координат математически формализуется в виде локального базиса, образуемого некомпланарными [23] векторами с условно единичной длиной:  r =
r =  ri = rij, который основан на смежных узлах расчетной сетки, образующих базисные векторы элементарного пространственного симплекса, в данном случае ‑ в абсолютной системе координат. Новый пространственный объект удобно называть геометрическим или базисным тензором 2-го ранга, или просто – тензором.
ri = rij, который основан на смежных узлах расчетной сетки, образующих базисные векторы элементарного пространственного симплекса, в данном случае ‑ в абсолютной системе координат. Новый пространственный объект удобно называть геометрическим или базисным тензором 2-го ранга, или просто – тензором.
В локальном координатном пространстве векторные объекты определяют не только геометрические свойства связанного базиса, но и задают характеристики сплошной среды, локализованной внутри и в ближайшей окрестности координатного трехгранника.
При определении векторных объектов, следует различать векторы, связанные с некоторой точкой пространства (точкой приложения), векторы, приложенные вдоль некоторой прямой, но не обладающие определенной точкой приложения, и, наконец, векторы, не связанные с определенной точкой приложения. Векторы, принадлежащие к первой группе, называются приложенными, или – определенными, ко второй – скользящими и к третьей [24] – свободными.
Операция сложения векторов может применяться только к числовым объектам, имеющим строго одинаковые физические размерности и при условии их определения строго в одном и том же координатном базисе. При соблюдении этих условий операция сложения применяется поэлементно к каждому векторному компоненту.
 A+
A+ B = ( Ax+Bx, Ay+By, Az+Bz ).
B = ( Ax+Bx, Ay+By, Az+Bz ).
К примеру, сложение определенных векторов сил приводит к вычислению равнодействующей силы [25], приложенной к этой же точке; сложение скоростей точки позволяет найти результирующий вектор скорости движения этой точки.
Более сложны те случаи, когда определенные векторы имеют различные точки приложения, а скользящие векторы приложены вдоль непересекающихся прямых. Для разрешения неопределенностей здесь могут быть дополнительно использованы модельные свойства сплошной среды, заполняющей пространство между разнесенными векторами.
Умножение векторов на скалярное число выполняется путем поэлементного перемножения векторных компонент с этим числом.
α· A = ( α·Ax, α·Ay, α·Az );
A = ( α·Ax, α·Ay, α·Az );
β· p = β·pij.
p = β·pij.
По физическому смыслу такое умножение можно определить как изменение масштаба объектов с векторными свойствами, при котором никак не изменяются пропорциональность векторных проекций, не изменяется ориентация векторов и базисных осей геометрических тензоров в пространстве.
Произведение векторов происходит в соответствии с правилами преобразования компонент базисных тензоров [26], определяющих особенности использования пространственных координатных систем.
Для двухстороннего преобразования векторных координат между локальным и абсолютным базисами, вводится понятие взаимного или контравариантного тензора [Кильчевский, 1954, с.35], обладающего свойствами дуального или сопряженного базиса [Астарита, 1978]. Поясним, что в матричном представлении такие тензоры являются взаимно обратными:  r =
r =  r-1.
r-1.
1. Объем координатного трехгранника вычисляется с помощью смешанного (векторно-скалярного) произведения базисных векторов:
Ω=  rx·(
rx·( ry ×
ry ×  rz),
rz),
 r :
r :
Ω= |  r | =
r | = 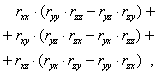
2. Преобразование для получения контравариантных компонент можно применить к базисным векторам ковариантного тензора:
 rx =
rx =  ry ×
ry ×  rz / Ω =
rz / Ω =  ;
;
 ry =
ry =  rz ×
rz ×  rx / Ω ;
rx / Ω ;
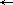 rz =
rz =  rx ×
rx ×  ry / Ω .
ry / Ω .
Контравариантные базисные векторы последовательно выстраиваются в качестве столбцов [28] соответствующей матрицы-тензора с проекциями компонент этих векторов в глобальной системе отсчета, как бы собираемой из элементов с транспонированными индексами, подтверждая тем самым правило для обращения простых матриц с размерностью (3´3), например, с использованием алгоритма алгебраических дополнений.
Это означает, что принятое правило тензорного построения локальных базисов, несмотря на произвольность их деформаций, позволяет точное и однозначное взаимное преобразование координатных отсчетов. Пары дуальных тензоров для взаимных преобразований между абсолютной и локальной системами координат, сами являются взаимно обратными, а их смешанные представления [29] – приводят к единичным тензорам:
 r ·
r ·  r =
r =  1 .
1 .
Отметим также, что аналогичное обращение ортогональных и ортонормированных (метрических) тензоров должно соответствовать простому транспонированию их матриц.
Геометрический смысл контравариантного тензора представляется как вычисление проекций единичных ортов абсолютной системы отсчета в координатной системе косоугольного локального базиса. В полной записи такое преобразование выражается как:
 r =
r = 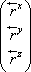 =
= 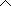 r-1=
r-1= .
.
При геометрической интерпретации локального (контравариантного) определения векторных проекций необходимо учитывать, что в локальной системе координат действует своя единичная мера, относительно которой должны вычисляться координатные отсчеты в таком внутреннем локальном базисе.
Пересчет векторных проекций между связанными системами координат выполняется с помощью операции произведения [30] с дуальными тензорами. В индексной форме операция полного тензорного умножения  a =
a =  a ·
a ·  r записывается в следующей форме ai = a j · rji , где индексы, стоящие при сомножителях на разных уровнях, называют немыми, а их появление в операциях произведения подразумевает суммирование векторных компонент по этому индексу:
r записывается в следующей форме ai = a j · rji , где индексы, стоящие при сомножителях на разных уровнях, называют немыми, а их появление в операциях произведения подразумевает суммирование векторных компонент по этому индексу:
 a =aj =
a =aj =  a ·
a ·  r =a i·rij = Si ( a i · rij ),
r =a i·rij = Si ( a i · rij ),
aj = a i · rij = ( ax ay az ) · 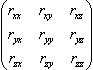 =
=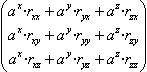 →
→  .
.
Как видно, при таком умножении уже не действует правило о выборе размерности результирующей матрицы, так как в результате преобразования вектора-строки из локального базиса, в абсолютной системе отсчетов получается вектор-столбец, и наоборот, вектор-столбец переходит в вектор-строку при преобразовании из абсолютной системы отсчета к локальному базису:
 a = ai =
a = ai = 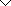 r ·
r ·  a = rij·aj =
a = rij·aj =  ·
· → ( ax ay az) .
→ ( ax ay az) .
В матричных преобразованиях с тензорами можно использовать условные правила о представлении свободных и базисных векторов в абсолютной системе отсчета в виде матриц-строк с размерностью (1´3), а контравариантных векторов ‑ в виде матриц-столбцов (3´1).
Аналогичные правила можно относить и к построению матриц для традиционных классов тензоров, в которых собственные векторы локального базиса, при их отображении на абсолютную систему координат, располагаются по строкам, а по столбцам – в обратной (дуальной) системе отсчета. В задачах механики сплошных сред столь же наглядная матричная компоновка трехмерных тензоров по правилам тензорной алгебры становится принципиально невозможной, так как в случае смешанных тензоров отсутствует соответствующее формальное представление для строк и столбцов матрицы.
Сами по себе операции векторно-матричных умножений не коммутативны. В индексной форме операция полного тензорного умножения:  a =
a = a ·
a ·  r записывается в следующей форме:
r записывается в следующей форме:
ai = ∑j ( aj · rji ) = ax ·rxi + ay ·ryi + az ·rzi . (9’)
Умножение может выполняться с повышением или понижением ранга результирующего произведения.
Так, например, в результате умножения вектора на тензор: rij · ak формируется вырожденный тензор третьего ранга qijk – с тремя индексами. Такие операции очень трудно истолковывать с позиций законов механики еще и потому, что в результате произведения получается существенно более сложный физический объект, для полного определения которого в простой операции умножения заведомо недостаточно информации, содержащейся в сомножителях более низкого ранга. Соответственно, такие операции не имеют особого физического смысла [31] , и никаких формальных обозначений для тензоров третьего ранга в этой книге не предусматривается.
Умножение с понижением ранга тензора, типа скалярного произведения векторов: q = ai·bi (проекция одного вектора на другой) обычно используется при анализе свойств вычислительных объектов [32]. Здесь и далее, все произведения пространственных числовых объектов построены так, чтобы ранг результата не изменялся.
Это означает, что в операциях произведения участвуют только числовые объекты с компонентами из разных (дуальных) базисов.
 [23] Компланарные векторы взаимно перпендикулярны одному общему вектору нормали
[23] Компланарные векторы взаимно перпендикулярны одному общему вектору нормали  ω, задающему ориентацию плоскости, в которой лежат все компланарные векторы. Тензорный базис на таких векторах называется вырожденным, так как его объем равен нулю, что и делает невозможным взаимно обратные преобразования векторов.
ω, задающему ориентацию плоскости, в которой лежат все компланарные векторы. Тензорный базис на таких векторах называется вырожденным, так как его объем равен нулю, что и делает невозможным взаимно обратные преобразования векторов.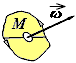 [24] Примерами определенных векторов являются скорости и ускорения материальной точки, а так же вектор силы приложенной к точке. Примерами скользящих векторов являются вектор силы, действующей на абсолютно твердое тело, и вектор его угловой скорости. Примером свободного вектора можно считать вектор момента пары сил, образующий свободную ось вращений
[24] Примерами определенных векторов являются скорости и ускорения материальной точки, а так же вектор силы приложенной к точке. Примерами скользящих векторов являются вектор силы, действующей на абсолютно твердое тело, и вектор его угловой скорости. Примером свободного вектора можно считать вектор момента пары сил, образующий свободную ось вращений  ω.
ω. [25] Операция сложения определенных векторов.
[25] Операция сложения определенных векторов. A =
A =  R +
R +  a ·
a ·  r .
r .