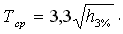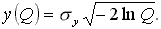§ 3. Проектные особенности корабля повышенной штормовой мореходности
Какой он все же, океан?
В нем нет ни чванства,
Ни парадности,
Когда он плавно волны катит
На зорьке -
Цвета спелой радости
И цвета грусти -
На закате.
Когда он тих
В своей безбрежности,
Тих,
Как ребенок за игрой, -
То он бывает
Цвета нежности
И цвета робости, порой.
Но если вдруг
Валы закружатся,
Зажав суденышко в кольцо,
То гневным,
Темным цветом мужества
Пронизано его лицо.
И ни следа от мудрой старости,
И ни следа - от доброты,
Когда в багровом цвете ярости
Он перейдет с тобой на <ты>.
Посмотришь на него,
Послушаешь -
И навсегда поймешь одно,
Что только цвета
Равнодушия
Ему природой не дано.
[Пантюхов И.М., 1975, стр 101] |
Древним корабелам-мореплавателям приходилось уделять существенно большее внимание безопасности штормового плавания, так как гребные весла непригодны в качестве движителей даже при умеренном волнении, а сильный шквальный ветер превращает парусное вооружение в источник серьезной опасности. Современное же судно при надежной работе главных двигателей и рулевого управления может противопоставить морской стихии мощность своих машин, тем самым снижая требования к штормовой мореходности, обеспечиваемые ранее за счет непротивления или пассивного снижения силового воздействия на корпус и надстройки корабля со стороны штормовых волн и ураганных ветров.
По выражению Томаса Джилмера [1984]: «Проектирование кораблей часто считают искусством...». Далее он продолжает: «... значение его как искусства недооценивается лишь теми конструкторами, воображение и творческая мысль которых ограничены...». Трудно отрицать такую мысль. При проектировании судовых обводов такое искусство будет актуальным вплоть до появления методов вычислительной оптимизации, учитывающей не только ходкость корабля на спокойной воде, но и весь комплекс вопросов штормового плавания на взволнованной поверхности моря. В настоящее же время удовлетворительных оптимизационных решений как в задаче о ходкости, так и в задаче о мореходности пока не обнаруживается. Пока нет надежных гидродинамических решений даже для поверочных расчетов по заданной форме корпуса, и не только в случае плавания на волнении, но даже и на спокойной воде.
Латинское слово projectus буквально означает – «брошенный вперед», что в техническом творчестве является поиском новых инженерных решений или созданием качественно новых технических объектов. Так же как и во времена возрождения Русского океанского флота во второй половине XIX века при адмирале И.А. Шестакове, интереснее было бы рассматривать вопросы проектирования новых кораблей с позиций хорошей морской практики, подразумевающей, по крайней мере, наличие плавценза у авторов новых или нетрадиционных решений по улучшению мореходных качеств корабля. А потому будут исключены из рассмотрения привычные методы «проектирования от прототипа», которые не могут соответствовать истинной сути термина «проектирование», так как невозможно «латанием старых прорех» получать качественно новые решения по достижению оптимальной мореходности кораблей.
Традиционно создание нового корабля образуется тремя ключевыми этапами работ, составляя эскизное, техническое и рабочее проектирование. Каждому из этапов соответствуют конкретные проработки концептуальных решений или рабочих чертежей и спецификаций, частные детали которых определяются как традициями кораблестроительных предприятий, так и особенностями планирования работ главными конструкторами проектов новых кораблей. Качество таких поисково-исследовательских работ всецело зависит от творческих способностей ученых и инженеров, участвующих в проектировании. Но все же можно попробовать определить общие вопросы, которые составляют тот минимальный комплекс
необходимых проектных условий, последовательное рассмотрение которых позволило бы разрешить множество противоречивых требований к новому кораблю.
О постановке задачи непротиворечивого проектирования
Проектирование, как наука о создании сложных технических сооружений, всегда оперирует частными инженерными решениями, что свидетельствует об отсутствии «достаточных условий» для поиска единственно верного или абсолютно оптимального проектного заключения. Это означает, что в проектировании почти всегда присутствуют элементы творчества, элементы непознаваемого авторского замысла.
Рассматривая корабль как единую и сложную инженерно-техническую систему, приходится также отмечать и отсутствие математически строгих формализаций или каких-либо других количественных критериев для постановки оптимизационной задачи о наилучшей форме корпуса и общекорабельной архитектуре. Именно это и означает, что мореходные качества корабля зависят от искусства проектирования, в котором, кроме строгих технических наук и формальной логики, необходимо также широкое использование практического опыта судовождения, в том числе и в сложных навигационных условиях эксплуатации кораблей и судов и заведомо маломореходных морских сооружений специального назначения.
Непротиворечивое или оптимальное проектирование может быть разделено на последовательные этапы комплексного изучения проблемы и согласования требований к кораблю как к сложной и единой инженерно-технической системе. Последовательность этапов образует направление исследований, формально определяемых как методы проектирования «сверху–вниз» (от общих требований к кораблю к частным техническим решениям по его конструкции), и «снизу–вверх» ( от доступных технологических возможностей к оптимальному по назначению проекту корабля в целом).
Комплексное решение задачи непротиворечивой оптимизации возможно в том случае, если удовлетворены все требования к кораблю как на проходе по логическим этапам «сверху–вниз», так и в строго обратном направлении «снизу–вверх».
Вариант проектирования нового корабля по принципу «снизу–вверх» традиционно используется при небольшом изменении тактико-технических характеристик или мореходных свойств хорошо зарекомендовавших себя кораблей или их серийных проектов. Фактически же это означает усовершенствование некоего «прототипа», а весь комплекс инженерно-конструкторских работ обычно сводится к поиску экономичных или технологичных вариантов постройки корабля, отработке оптимальных вариантов установки нового судового оборудования и, при необходимости, экспериментальному опробованию небольших новаций по управлению кораблем в сложных и особых условиях плавания. Корабль является настолько сложным инженерным сооружением, что этап проектирования «снизу-вверх» в полной мере присутствует даже при закладке многократно повторяемого серийного образца, что связано с естественным совершенствованием, как кораблестроительных технологий, так и с обновлением судовых механизмов, навигационного оборудования и условий судоходства на международных морских путях.
На этапе проектирования «снизу – вверх» всегда отрабатываются наилучшие или оптимальные проектные решения, которые соответствуют современному состоянию кораблестроительных наук и технологий.


Логическая схема поискового (слева) и поверочного (справа) этапов непротиворечивого проектирования нового гипотетического корабля, показывающая последовательность согласования технических решений и их взаимосвязь с эксплуатационными требованиями к кораблю повышенной штормовой мореходности. Левая матрица показывает разделение комплекса требований к кораблю на три независимых направления исследований, образующих троичную матрицу последовательного поиска и согласования непротиворечивых проектных решений. Направление по столбцам сверху вниз соответствует переходу от теории к практике, по строкам слева направо – от анализа общих вопросов к конкретным техническим решениям. Правая матрица образует комплекс поверочных задач, которые должны быть изучены мореплавателями, ответственными за эффективное использование корабля, а также оптимальность и экономичность его эксплуатации в составе флота, на конкретных морских путях. На этапах эскизного проектирования корабля, при разработке законченных инженерных решений и на последующей опытной эксплуатации нового корабля вновь и вновь необходимо рассматривать аналогичные по структуре и составу проектные матрицы, что позволит согласовать все технические решения и задачи эффективного использования корабля в течении всего срока его службы.
Но все же принципиально новые или нетрадиционные корабли могут появиться только исходя из принципов проектирования «сверху – вниз», когда из общих проектных предпосылок или ничем не подкрепленных пожеланий мореплавателей делается попытка найти конкретные технические решения и согласовать даже самые немыслимые технологические и будущие эксплуатационные противоречия, сохраняя при этом все принципы «хорошей морской практики» и не усложняя безмерно кораблестроительные технологии или условия эксплуатации будущего корабля.
Из анализа мореходных качеств исторических кораблей можно сделать вывод о существовании своеобразного системного подхода, связанного замкнутой системой проектного анализа инженерно-технических решений и эксплуатационных требований к всепогодному кораблю, которые ныне воспринимаются только как комплекс забытых или «неписаных» правил «хорошей морской практики».
Полагая, что проектные противоречия могут быть замкнуты в троичном логическом базисе, основанном на задачах (как глаголах) и решениях (как существительных), или в логическом пространстве этапов проектирования как «времени»–«существования» и «пространства»–«явления», в которых отражаются эксплуатационные требования и технологические возможности при создании нового корабля.
Таким образом, элементы проектирования сложных инженерных систем будут формализованы в виде трехмерного логический базиса, оси которого станут служить проекциями для отметки выполнения основных инженерно-технических задач и по которым возможен контроль непротиворечивости проектных решений в целом, и в том числе по форме корпуса и связанной с ней общекорабельной архитектуре. По аналогии с построением сложных вычислительных экспериментов в корабельной гидромеханике, в качестве базисных осей проекта могут быть выбраны независимые друг от друга логические направления проектных исследований, которые формально могут быть связаны следующими терминами:
1) «время» как наука управления кораблем в сложных или в штормовых условиях плавания, основные положения которой должны неукоснительно соблюдаться либо чисто техническими средствами, либо строгими навигационными наставлениями по эффективному управлению кораблем и безопасности мореплавания;
2) «пространство», или способность активного существования корабля в заданном физическом окружении, что в реальности соответствует тому обширному кругу морских задач, боевых или коммерческих операций, которые корабль обязан выполнять в любой, даже в самой сложной навигационной обстановке, при частичных повреждениях корпуса и аварийных поломках судового оборудования;
3) «проект», или обобщенные инженерно-технические задачи, реализованные в конструкции и техническом вооружении корабля, технологических решениях при его строительстве и условиях эксплуатации, в навигационном обеспечении и поддержании ремонтной базы, возможностях обновления и модификации судового оборудования.
Может быть, для исторического анализа конкретного класса океанских кораблей применение троичного базиса выглядит несколько искусственным. Но эта матрица может объяснить разнообразие проектных решений, принимаемых корабелами различных стран, прежде всего, если принимать в рассмотрение основное предназначение корабля (п.3), условия его плавания (п.2) и особенности эксплуатации флота конкретной страны (п.1).
Если целью оптимизации выбрана стабилизация корпуса корабля при плавании в условиях интенсивного морского волнения, что является важнейшим требованием боеспособности артиллерийских кораблей, то на примере анализа технических решений по принципу «сверху – вниз», проектирование корабля может быть разделено на три строго последовательных во времени этапа исследований:
1 этап. Скалярный. Определяется основное назначение или тип корабля, который описывается «линейным» набором (перечислением) требований. Такие требования редко бывают непротиворечивыми.
2 этап. Векторный. Каждое из требований к кораблю формализуется внутри своеобразного проектного базиса, в котором каждое направление исследований является независимым, математически–ортогональным. В зависимости от этапа проектирования (или типа корабля) базисные направления могут быть различными. Так, в случае поиска непротиворечивых решений для корабля повышенной штормовой мореходности базисными направлениями могут стать:
2.1. Ходкость, в том числе на волнении;
2.2. Стабилизация корпуса при плавании и маневрировании на волнении;
2.3. Безопасность мореплавания в штормовых условиях и в аварийных ситуациях, в том числе при повреждениях корпуса.
На векторном этапе исследования остаются взаимозависимыми, и главной целью логического проектирования является качественная оценка этой зависимости.
3 этап. Тензорный (матричный). Здесь уже не разрабатываются новые технические решения, но анализируются по формальному признаку проработанные на втором, векторном этапе. Выстроенные в виде троичной логической матрицы новые технические решения должны допускать «операцию обращения», по форме похожую на обращение математической матрицы.
Если обратная матрица существует и сохраняет логическую связь между проектными элементами, то весь комплекс новых технических решений снова формализуется в виде скалярной точки отсчета и обратного логического базиса, задающего направления векторного анализа «снизу вверх»: от имеющихся научно-технических и технологических возможностей к оптимальному кораблю по условиям эффективности, экономичности и безопасности штормовой эксплуатации.
При возврате к исходному уровню скалярный этап становится тензорным, допускающим анализ достаточности принятых в самом начале решений: удовлетворяют ли полученные новые проектно-технические решения основному предназначению нового корабля?
Так получается, что на начальных этапах проектирования по пути «сверху вниз» имеются только необходимые предпосылки для поиска непротиворечивых решений о новом гипотетическом корабле повышенной штормовой мореходности, наиболее приоритетными из которых могут быть признаны: ходкость и стабилизация корпуса на интенсивном волнении при безусловном обеспечении безопасности мореплавания. Методически и инструментально независимыми направлениями проектных исследований можно выбрать: изучение исторического опыта мореплавания и неписаных правил «хорошей морской практики»; поверка новых и ключевых технических решений эвристического характера с помощью современных математических моделей и ранее выполненных исследований мореходности; проведение сравнительных и специализированных опытовых экспериментов с моделями судов, результаты которых могут быть использованы для формирования конкретных инженерных решений о формировании общекорабельной архитектуры нового корабля. При разделении каждого направления на три группы последовательно решаемых задач будет сформирована искомая троичная матрица, совместная разработка элементов которой образует процесс непротиворечивого проектирования нового гипотетического корабля.
По завершению проектного этапа возникает концептуальное построение нового корабля, который можно охарактеризовать как нетрадиционный в целом или в основных элементах его архитектуры. В этом случае становится актуальным столь же комплексный поверочный анализ принятых технических решений с эксплуатационных позиций, по результатам которого возможно заключение об оптимальности нового проекта корабля: его эксплуатационной и экономической эффективности.
В зависимости от класса и назначения корабля выбирается метод исследования основных элементов будущего корабля, которые должны образовывать единую систему согласованных инженерно-технических решений. В любом случае при проектировании судна детально изучаются следующие вопросы:
- принятие решения о форме корпуса корабля и особенностях общего расположения судовых механизмов и помещений, предварительное изучение особенностей ходкости, остойчивости, непотопляемости, штормовой мореходности и безопасности плавания нового судна;
- распределение нагрузки и соотношения весов вдоль корпуса и по уровням палуб, удифферентовка и определение соотношений между судовыми запасами, полезной нагрузкой и вместимостью судна, согласование вариантов и минимизация объемов балластировки при различной эксплуатационной нагрузке судна;
- отработка вопросов ходкости и качки судна в условиях штормового волнения, согласование методов борьбы за живучесть судна в аварийных ситуациях, в том числе при остановке машин в штормовых условиях;
- повторное уточнение формы корпуса и общекорабельной архитектуры, достаточное для проведения проектных расчетов остойчивости, плавучести и непотопляемости в различных режимах плавания, в том числе в аварийных ситуациях и при затоплении отсеков корпуса судна;
- принятие заключений о конструктивных особенностях корпуса судна, о типе и расположении главных двигателей, об управляемости в различных условиях эксплуатации, об удовлетворительной обитаемости в штормовых условиях плавания.
Требования к проектированию иногда усложняются дополнительными задачами, такими как обеспечение ледового плавания или необходимость учета особенностей использования судна в военное время, иной раз предусматривается возможность переоборудования судна для изменения его назначения.
Теоретическое изучение волновых процессов
Современные математические модели корабельного волнообразования и взаимодействия корпуса корабля с морским волнением не позволяют получить законченных численных решений об оптимальной форме корпуса, что связано со слабой разработанностью трехмерных моделей вычислительной гидромеханики. Построение многовариантных процессов оптимизации формы корпуса с использованием сложных численных схем для решения трехмерных задач гидромеханики со свободными поверхностями также затруднительно из-за ограниченных мощностей современных компьютеров.
Аналитическое изучение волнового сопротивления корабля берет свое начало от работ Джона Генри Мичелла [Michell J.H., 1898], где был предложен “вполне” определенный интеграл, с указаниями на допущения о малости возмущений, вносимых движущимся узким корпусом корабля [Павленко, 1953]:
 (1)
(1)
где: f = f( x,z ) – ординаты формы корпуса; V0 – скорость корабля; Ω - элементарная площадка на обшивке корпуса; φ = arccosV/V0
- фазовый угол Кельвина, задающий направление излучения (отражение) корабельных волн с частотой формы волны: k=g /( V02·cos2J ) .

Рис. 1. Геометрическая интерпретация классического интеграла Мичелла показывает процесс отражения внешних волн от диаметральной плоскости «узкого» корабля. На реальном же корпусе происходит существенное искажение фазовых и частотных свойств излучаемых волн. В оконечностях корпуса, вне интервала А-В, излучения волн не происходит. φ — угол излучения (отражения) корабельной волны; V0 — скорость хода судна.
Физико-геометрическая интерпретация и анализ существования численных решений при моделировании гидродинамических процессов в интегралах Мичелла показывают, что в реальности этими уравнениями описывается процесс отражения от корпуса корабля внешних волн (рис. 1) в диапазоне длин: l Î [ 0
¸ L = 2×p×V02/g], что соответствует первой половине фазового угла: J Î 0
¸ p /2, в то время как недостающая для замыкания интеграла четверть горизонта: J Î π /2
¸ p определяет падающую на корпус «внешнюю волну». Следовательно, математическая оптимизация подводных обводов и надводной формы корпуса корабля по сути является поиском технических решений, обеспечивающих прохождение штормовой волны через корпус с минимальными искажениями.
То есть для недопущения отражения штормовой волны от бортовой обшивки корпуса и для ослабления передачи волновой энергии на опасное усиление рыскания и качки корабля необходимо оптимизировать волновое сопротивление на всех скоростях хода, включая высокоскоростные режимы с числами Фруда: Fn³0,5, на которых происходит образование корабельных волн с такими же параметрами, как и внешнее морское волнение (аналогичные решения по оптимизации обводов корабля и его надводного облика способствуют скрытности в лучах гидро- и радиолокаторов).
Следовательно, справедлив вывод о том, что минимизация волнового сопротивления корабля на всех скоростях хода, включая закритически высокие, одновременно будет обеспечивать минимизацию силового взаимодействия корабля с внешним морским волнением. Аналогичный вывод иллюстрировался в технико-историческом анализе мореходности (§ 1) с помощью простых геометрических построений процессов взаимодействия корпуса корабля и морского волнения.
Рис. 1 показывает также, что аналитическое представление процесса «отражения» внешних волн от движущегося корпуса корабля не вполне адекватно учитывает реальную картину корабельного волнообразования, так как «теоретически» регулярные внешние волны при отражении от широкого корпуса корабля претерпевают очень сильные частотные (доплеровские) искажения, а в оконечностях корпуса происходит не отражение, а накопление волновой энергии. Соответственно, для корректного учета особенностей корабельного волнообразования снова необходимо искать инженерные (эвристические) подходы с использованием геометрической и динамической интерпретации потоков жидкости вблизи корпуса, особенно в его оконечностях.
Математическая оптимизация подводных обводов и надводной формы корпуса и надстроек корабля, по сути, является поиском технических решений, обеспечивающих прохождение штормовой волны через корпус с минимальными искажениями. Однако аналогичные математические модели описывают отражательные свойства формы корпуса под воздействием гидроакустических или радиолокационных волн, откуда следует дополнительное предположение, что оптимизация штормовой мореходности способствует скрытности корабля в море, а исторические корабли начала XX века удовлетворяли требованиям современных стеллс-технологий.
Основные обозначения и соотношения кинематики корабельных волн
| { x, y, z } |
Координаты в связанной с корпусом системе координат (СК); |
| { xо,yо,zо } |
Точка, лежащая на поверхности корпуса; |
| { x, h, V } |
Координаты в СК неподвижной относительно жидкости на бесконечности; |
| { x0,h0, V0 } |
Точки, лежащие на свободной поверхности взволнованной жидкости; |
| V0 |
Скорость набегающего потока [м/c]; |
 |
Число Фруда (скорость относительно продольной волны); |
| λ/L = 2p·Fn2 |
Отношение длины поперечной волны, излучаемой кораблем к длине его корпуса, выраженное с помощью числа Фруда; |
 |
Частота формы волны [1/м]; |
| C=V0·cos2φ |
Скорость волны, излучаемой корпусом, в направлении ÐJ [м/c]; |
| φ=arccosV/V0 |
Фазовый угол Кельвина, задающий направление распространения “плоских” волн, образуемых корпусом корабля на частоте излучения параметра φ; |
| V=V0cosφ |
Скорость распространения корабельной волны в направлении φ; |
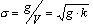 |
Частота волновых колебаний (во Времени) [1/c]; |
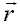 |
Отклонение частицы жидкости от ее невозмущенного состояния [м]; |
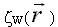 |
Аппликаты волнового профиля [м]; |
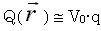 |
Интенсивность распределенных по поверхности корпуса особенностей, моделирующих движение в безграничной жидкости [м/c]; |
| s2 = Ω2= g·k |
Дисперсионное соотношение для волн на глубокой воде; |
| λ = g·T2 / 2 π = С2·2 π/g |
Соотношение между длиной, периодом и скоростью движения гребней волн на глубокой воде [м]. |

Рис. 2. Система координат.
Интеграл Мичелла далеко не исчерпал своих аналитических возможностей, и в случае углубленной физико-геометрической интерпретации его подынтегральных выражений, возможен не только уточненный расчет волнового сопротивления корабля, но и качественный анализ волнообразования в непосредственной близости к обшивке корпуса, в том числе с целью оптимизации формы судовых обводов.
Сам же интеграл Мичелла содержит довольно сложные сингулярные и осциллирующие подынтегральные выражения, которые без применения специальных аппроксимационных и асимптотических методов оказываются недоступными для уверенных вычислений на современных цифровых ЭВМ.
Существуют различные методы получения интеграла для расчета волнового сопротивления по Мичеллу, которые пока не будут рассматриваться здесь. Основная цель рассмотрения этой линейной теории волнового сопротивления состоит в поиске наглядной геометрической и физической интерпретации вычислительных процессов, моделирующих корабельное волнообразование. Понимание же основы и сути моделируемых явлений необходимо для построения уточненных полуэмпирических моделей и формул, учитывающих свойства реальных корабельных волн, что очень важно, так как процессы волнообразования, равно как и процессы вихреобразования, всегда нелинейные.

Рис. 3. Характерная картина волнообразования при равномерном и прямолинейном движении судна по спокойной поверхности воды. (λ / L) =0,5; V=13 узлов. За кормой отчетливо просматривается система поперечных корабельных волн, ограниченная треугольником свободных расходящихся волн.
Традиционно корабельные волны разделяются на поперечные и расходящиеся, что соответствует наблюдениям за внешним проявлением волнообразования при движении корабля. В непосредственной близости от корпуса корабля такое разделение корабельных волн на поперечные и расходящиеся весьма условно, однако оно вполне справедливо при рассмотрении особенностей распространения волн на большом удалении от корпуса, где поперечные волны ведут себя как вынужденные, а расходящиеся - как свободные, с ярким проявлением особенностей их групповой структуры.
В случае хорошо обтекаемого корпуса справедливо также допущение о стационарности формы волнового поля относительно движущегося корабля, что является ключевым упрощением особенностей реального корабельного волнообразования, используемого при теоретическом изучении волнового сопротивления его движению.
Плоская модель поперечных волн
Плоская модель корабельного волнообразования рассматривает интерференцию зарождающейся поперечной волны при прохождении потоков воды вдоль корпуса корабля и позволяет сделать самые первые оценки процессов зарождения корабельных волн.
Вне зависимости от формы корпуса за кормой корабля образуется регулярная система поперечных корабельных волн, длина и период которых строго связаны со скоростью хода корабля :λW = V02·2 π /g; t W = V0·2 π /g.
Такое свойство системы поперечных волн позволяет довольно просто оценить реальную скорость хода корабля V , воспользовавшись визуальным соотношением расстояния между гребнями волн λ и длиной корабля L : (λ /L) = V2/ L ·2 π/g, откуда:
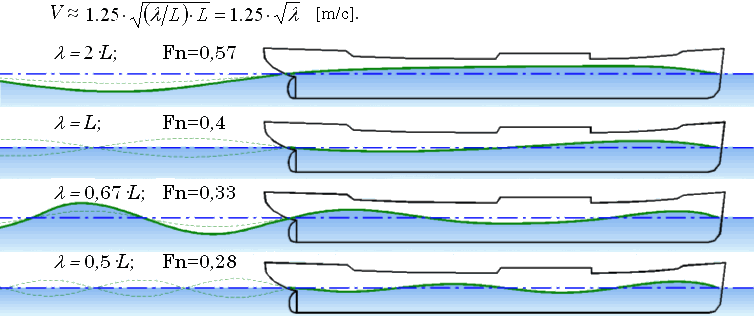
Рис. 4. Характерные режимы волнообразования при различных скоростях движения судна.
В качестве безразмерного и независимого от длины корпуса параметра, характеризующего волнообразование на различных скоростях хода корабля, принято число Фруда:

которое также связано с отношением длины поперечной волны к длине корпуса корабля: (λ/L) = 2p·Fn2
или

Теоретически получается, что при длине поперечной корабельной волны, строго равной длине корпуса, может ожидаться наиболее благоприятная интерференция носовой и кормовой систем волн. Однако на практике реальная волнообразующая длина корпуса всегда меньше, отчего искомый минимум волнового сопротивления уменьшается со значения Fn≈0,4 до Fn≈0,32–0,36, соответствующий рост волнообразования на скорости хода при Fn≥0,57 обычно соотносят с Fn≥0,5.
К сожалению, величину волнообразующей длины корпуса довольно трудно установить однозначно, так как она зависит от изменения скорости хода корабля. Рис. 4 иллюстрирует интерференцию корабельных волн, условно зарождающихся на форштевне и ахтерштевне. В реальности же носовая подпорная волна зарождается в районе скулы, а снижение уровня воды в кормовой части корпуса проявляется в районе кормовой раковины и винто-рулевого комплекса, что обязательно необходимо учитывать при проектировании обводов корпуса. Необходимо также отметить, что на больших скоростях хода, при Fn>0,4, в кормовой части корпуса образуется довольно сильное разрежение, которое при совместном действии с носовой подпорной волной приводит к сильному ходовому дифференту корабля на корму. При дальнейшем увеличении скорости судно как бы начинает толкать перед собой «гору» воды, отчего быстро растет как интенсивность корабельного волнообразования, так и волновое сопротивление движению корабля. Однако эффект столь неблагоприятной интерференции носовой и кормовой систем корабельных волн может быть частично скомпенсирован специальной формой корпуса, ключевым элементом которой должен являться завал бортов на уровне действующей ватерлинии в средней части корпуса.

Рис. 5. Характерная форма и числовые оценки расчетных кривых волнового сопротивления для хорошо обтекаемого корпуса корабля. Сx – коэффициент сопротивления; Rx/D – удельное сопротивление. Хорошо видны экстремумы сопротивления при неблагоприятной интерференции носовой и кормовой систем поперечных волн, возникающей на скоростях хода при Fn≈0,5 (0,57) и Fn≈0,3 (0,33). Полного гашения волнового сопротивления при Fn≈0,26 (0,28) и Fn≈0,35 (0,4) не происходит, что объясняется затратами энергии на зарождение системы расходящихся волн.
Для оценки сопротивления воды движению корабля обычно пользуются величиной коэффициента сопротивления СW, отнесенного к квадрату скорости и площади смоченной поверхности (подводной части) корпуса.

где: RW – волновое сопротивление [Н]; ρ - плотность жидкости [кг/м3]; V – скорость хода судна [м/с]; S – площадь смоченной поверхности корпуса.
Для оценки формы корпуса и волнового сопротивления иногда удобно пользоваться размерной величиной удельного сопротивления, отнесенного к водоизмещению корабля: RW / D, где D – водоизмещение [кг].
Если тихоходное судно (Fn≤0,2) обладает хорошо обтекаемым корпусом, то его волновое сопротивление будет пренебрежимо малым.
Особенности расходящихся корабельных волн
Расходящиеся от корпуса корабельные волны проявляются как свободные волны на глубокой воде, они обладают как ярко выраженными дисперсионными свойствами (увеличение длины и периода волны при ее свободном распространении), так и групповыми свойствами (скорость распространения волнового возмущения в два разе меньше скорости движения фронта каждой из волн, образующих волновой пакет).
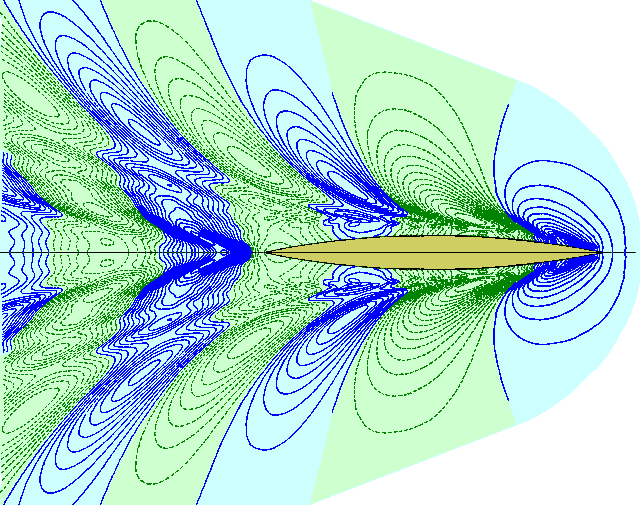
Рис. 6. Картина корабельного волнообразования в непосредственной близости от обшивки корпуса. Скорость хода Fn=0,316.Синими линиями отмечено повышение уровня свободной поверхности, зелеными – понижение.
Угол расхождения пакетов корабельных волн не зависит от скорости хода корабля и является ярким подтверждением того, что пакеты свободных расходящихся волн движутся со скоростью в два раза меньшей, чем гребни составляющих их волн. Этот угол составляет 20°42’. В 1887 Кельвином получено также решение для корабельных волн от точечного источника на поверхности воды, угол разворота гребней расходящихся волн составил 35°16’. Любопытно, что Кельвин также использовал эвристический аргумент, основанный на групповой скорости волн [Дж.Ньюмен, 1985].
К расходящейся корабельной волне неприменимы методы интерференционного анализа. Единственный способ минимизации энергии расходящейся волны - это построение таких обводов корпуса, которые способствовали бы ее гашению непосредственно в момент зарождения. Обычно это достигается «закручиванием» набегающего потока под днище корпуса в тот момент, когда вихрь зарождающейся волны начинает отрываться от корпуса. Привычные скуловые обводы в носовой и кормовой частях корпуса вполне успешно могут решить задачу минимизации таких расходящихся волн.
Предварительный обзор особенностей корабельного волнообразования можно закончить двумя заключениями, имеющими прямое отношение как к минимизации волнового сопротивления, так и к уменьшению интенсивности силового взаимодействия корпуса корабля с внешним морским волнением:
- минимизация интенсивности поперечных корабельных волн на всех скоростях хода, включая диапазон их длин, превышающих длину корпуса, выполненная на всех осадках, которые возникают при вертикальной качке корабля, одновременно является условием снижения его килевой качки при движении на волнении;
- аналогичная минимизация интенсивности расходящихся корабельных волн будет способствовать снижению бортовой качки, возникающей под воздействием штормовых волн в широком диапазоне периодов.

Рис. 7. Крейсер «Москва» имеет обводы в форме двойного клина и сильный развал бортов вдоль всего корпуса корабля. |
Высказанные заключения являются всего лишь проектными условиями, выполнение которых безусловно необходимо, но отнюдь не достаточно для реального улучшения штормовой мореходности корабля. К примеру, в практике кораблестроения известны примеры использования судовых обводов в форме «двойного клина». «Двойной клин» раздвигает встречный поток в боковые стороны, а под широкий кормовой подзор поток воды поступает из-под днища корпуса. Такие обводы формально приводят к заострению оконечностей, что теоретически влияет на корабельное волнообразование как удвоение длины корпуса, что заметно снижает волновое сопротивление движению корабля. Однако в отличие от традиционного корабля с симметричным относительно мидель-шпангоута обводами, в штормовых условиях корпус в виде «двойного клина» может стать источником серьезнейшей опасности.
До настоящего времени неизвестны достаточно обоснованные математические модели корабельного образования, кроме интеграла Мичелла, которые могли бы использоваться для уверенного проектирования обводов корпуса. Попытка использовать этот интеграл в качестве функционала для выбора оптимальной формы корпуса не приводит к сколь-нибудь однозначным решениям, так как при математической недостаточности внешних условий для формализации судовых обводов получается множество частных решений, иногда курьезных, дающих в качестве оптимальной формы корпуса как «двойной клин», так и различные пульсирующие формы ватерлиний с гиперболизованными размерами носовых бульбов.
Но все же решение Джона Генри Мичелла представляет не только исторический интерес. Детальный анализ промежуточных выкладок при получении интеграла Мичелла позволяет очень глубоко понять суть процессов, происходящих как при формировании корабельных волн, так и при воздействии штормовых волн на корпус корабля.
В настоящее время существуют и другие математические и вычислительные методы для получения результатов, аналогичных Мичелловским, но это уже тема других работ по гидромеханике корабля, в том числе требующих множества новых пионерских исследований. Пока же постараемся не слишком далеко отклоняться от формы и сути математических изысканий конца XIX века, попутно пытаясь привести все выражения к размерным физическим аргументам и функциям, что необходимо для углубленного понимания изучаемых процессов волнообразования и требуется для корректной реализации численных расчетов волнового сопротивления корабля.
Теория волнового сопротивления Мичелла
Основная цель рассмотрения линейной теории волнового сопротивления состоит в поиске наглядной геометрической и физической интерпретации вычислительных процессов, моделирующих корабельное волнообразование. Это необходимо также для поиска аналитических решений, корректных асимптотических приближений и эмпирических экстраполяций при практическом моделировании процессов взаимодействия корабля и морского волнения.
Оригинальный интеграл Мичелла вполне пригоден для использования в областях разрывных или сильноосциллирующих численных решений, нежели любые его искусственные усложнения с помощью любых нелинейных добавок.
Волнообразующий потенциал
Вывод расчетных формул классической теории волнового сопротивления корабля основывается на анализе скалярных функций векторного аргумента или «теории потенциала»:
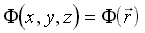 . Решение ищется в виде поля скалярного потенциала скорости:
. Решение ищется в виде поля скалярного потенциала скорости: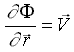 , удовлетворяющего уравнению Лапласа:
, удовлетворяющего уравнению Лапласа:
 1
1
Для исследования волнообразования, вызванного равномерным поступательным движением корабля, пересекающего свободную поверхность жидкости, используем стандартное аддитивное разложение потенциала [Костюков А.А., 1966]:
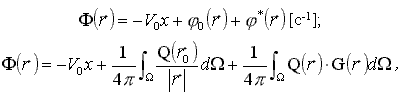 (2.0)
(2.0)
где: V0x потенциал набегающего потока;
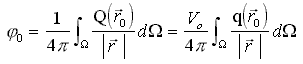 (2.2)
(2.2)
потенциал обтекания корпуса при отсутствии возмущения свободной поверхности;
 (2.3)
(2.3)
потенциал, учитывающий взаимодействие корпуса со свободной поверхностью жидкости.
Величина Q0=V0·q соответствует интенсивности распределенных по поверхности корпуса источников, которые моделируют условие непротекания при движении корпуса корабля в безграничной жидкости.
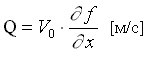 ( 3 )
( 3 )
где: f(x,z) - ординаты корпуса. Использование функции Q в интеграле (2.3) накладывает условие малости искажений формы свободной поверхности вблизи корпуса.
Под функцией G будем понимать потенциал некоторого единичного возмущения свободной поверхности от источника, лежащего на элементарной площадке, расположенной на поверхности корпуса корабля. Тогда функция 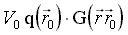 будет определять потенциал течения, обусловленного влиянием источников, распределенных по всей поверхности корпуса, на свободную поверхность пересекаемой им тяжелой жидкости.
будет определять потенциал течения, обусловленного влиянием источников, распределенных по всей поверхности корпуса, на свободную поверхность пересекаемой им тяжелой жидкости.

Рис. 8. Движение точечного источника (шарика) по поверхности воды. Образуются расходящиеся корабельные волны, длина которых соизмерима с диаметром шарика. Поперечные же волны, скорость которых соответствует скорости движения источника возмущения, практически не образуются, и просматриваются только один раз в виде одиночного всплеска в следе за шариком. Расходящиеся гравитационные волны постоянно изменяют фазу своего переднего фронта, показывая, что волновое возмущение в целом движется в два раза медленнее, чем фронт одиночной трохоидальной волны. Впереди основных волн выстраиваются фронты коротковолновых капиллярных возмущений, скорость распространения которых выше, чем у гравитационных волн.
Аддитивное разложение потенциала [Костюков А.А., 1966] можно считать справедливым, если рассматриваются волновые движения, вызванные идущим кораблем, вдали от его корпуса, где потенциал j0 стремится к нулю и не оказывает влияния на динамические граничные условия на свободной поверхности. Соответственно влияние функции G должно быть настолько малым, чтобы ей можно было пренебречь при выполнении условий непротекания на поверхности корпуса в решении для потенциала φ0.
Сформулируем исходные уравнения и граничные условия:
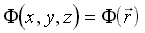 ( 2’ )
( 2’ )
потенциал течения в системе координат, связанной с корпусом;
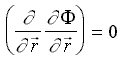 ( 4 )
( 4 )
уравнение Лапласа, как условие существования потенциала и достаточное условие для обеспечения неразрывности жидкости;
 ( 5 )
( 5 )
условие непротекания на поверхности корпуса для потенциала Ф0 = -V0 x + φ0;
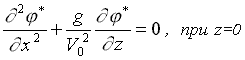 ( 6 )
( 6 )
линейное динамическое граничное условие на свободной поверхности, которое получается из интеграла Эйлера по условию постоянства давления вдоль линии тока, лежащей на свободной поверхности;
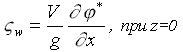 (7)
(7)
описание профиля волны. Следует из (6);
 (8)
(8)
условия на бесконечности.
Волнообразующий потенциал G должен обеспечивать свойство симметрии относительно диаметральной плоскости корпуса, что может являться следствием определения распределенных источников Q (x,z) и считаться справедливым только для узкого корпуса. Такое же допущение делалось Мичеллом при выводе интеграла (1).
Так же как Мичелл используем интенсивность распределенных источников в форме:  , а волнообразующий потенциал как:
, а волнообразующий потенциал как:
 (2.3’)
(2.3’)
Граничные условия и интегральное преобразование Фурье
Предположим, что граничное условие на свободной поверхности удовлетворяется для каждого элемента свободной поверхности dΩ, содержащего волнообразующий потенциал q·G. Это будет означать также удовлетворение условий малости возмущений свободной поверхности от единичного волнообразующего потенциала G, действующего с элементарной площадки dΩ, в то время как суммарное влияние всего корпуса может быть достаточно большим.
Также как в справочнике по теории корабля под редакцией Я.И. Войткунского [1985] будем искать решение для G в форме отраженного через свободную поверхность стока, то есть в виде потенциала от зеркально отраженного источника с обратным знаком. Тогда функция G не имеет особенностей и непрерывна во всей области z і 0, кроме случая, когда z=z0=0, то есть на свободной поверхности и когда волнообразующий источник находится на этой же поверхности.
Пусть: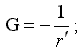 (9)
(9)
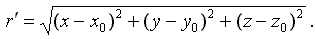 .
.
Используем интегральное преобразование Фурье для функций трех переменных:
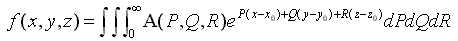 (10)
(10)
Удовлетворяя уравнение Лапласа (4) для функции 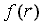 , получим:
, получим: 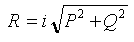 .
.
После введения обозначений: P =k·cosJ ; Q = k·sinJ , возможен переход к представлению источника
1/r‘ в виде интеграла Фурье, зависящего от двух параметров:
 (11)
(11)
В формуле (11) последнее слагаемое для Ω взято из Дж.Ньюмена [1985], и отвечает за волны нестационарные по отношению к корпусу.
По физическому смыслу - экспонента под интегралом в формуле (11) описывает некие плоские волны в связанной с корпусом системе координат { x,y,z }, эти волны стационарны относительно движущего корпуса и ориентированы в направлении угла φ.
Пусть: G* = e k·(-z-z0-iw ). (12)
Подставляя G* в динамическое граничное условие на свободной поверхности: 
Тогда: 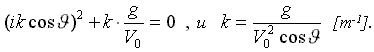 (13)
(13)
После установления зависимости между параметрами k и φ в интеграле (11), можно избавиться от одного параметра интегрирования. С этой целью применим интегрирование по частям:  .
.
При изменении порядка интегрирования во втором интеграле:  внутренний интеграл, по параметру φ обращается в нуль:
внутренний интеграл, по параметру φ обращается в нуль:
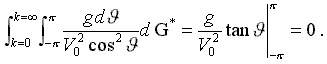 .
.
Тогда волнообразующий потенциал G может преобразуется к следующему виду:
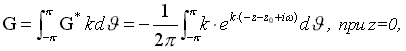 (14)
(14)
где: 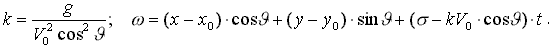
Описание единичного волнообразующего источника
Воспользуемся описанием профиля корабельной волны (7) для получения общей волновой картины от движущегося источника, который описывается только что полученным интегралом (14):
 (15)
(15)
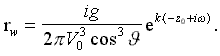 (16)
(16)
Аппликата свободной поверхности для заданной частоты формы волны:
 (17)
(17)
Аппликата волновой поверхности от возмущения, вызванного элементарной площадкой судовой обшивки:
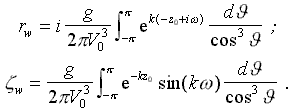
Теперь необходимо воспользоваться требованием стационарности картины волнообразования относительно системы координат, связанной с корпусом корабля.
1. Если s связана с k дисперсионным соотношением:
 (18)
(18)
то в функции G* пропадает величина: 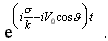
2. Скорость движения излучаемой корпусом волны не может превышать скорости хода корабля: V £ V0 .
Тогда, если V0 cosφ, что следует из (13), то: V=0 соответствует φ = ± π /2 ; V=V 0 соответствует
φ = 0 или φ= ± π.
Геометрическое толкование уравнения (17) изложено в книге Г.Е. Павленко [1952], где показывается система трехмерных свободных волн, распространяющихся с фазовой скоростью V=V0 cosJ в направлении угла ÐJ.
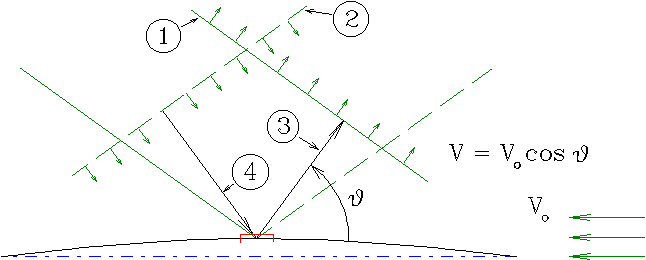
Рис. 9. Полная схема отраженного излучения корабельных волн и положение их фронтов. (1) фронт расходящейся волны (излучаемой), движущейся со скоростью V=V0
cosφ; (2) положение фронта волны, приближающейся к корпусу корабля, которая также является стационарной в связанной системе координат, но не учитывается в наших динамических уравнениях;(3) направление излучения расходящейся корабельной волны; (4) направление подхода как бы внешней волны, у которой угол
ÐJ лежит в диапазоне: ÐJÎ] - π/2 ¸ -p] или ÐJÎ[p ¸ p/2[.
Исходя из анализа рисунка 9, будем считать возможным искусственное ограничение интервала интегрирования в определении волнообразующего потенциала (14), до: ÐJÎ]- π/2 ¸ -p], тогда:
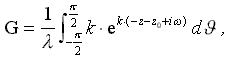 (14’)
(14’)
где: 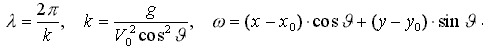
Таким образом, из рассмотрения исключаются свободные волны, которые допускаются динамическим граничным условием (6). Это именно те волны, которые можно интерпретировать как внешние и поглощаемые корпусом корабля при взаимодействии с морским волнением. Если корпус корабля способен поглощать внешние волны, то их энергия уходит на усиление качки и рыскания. Из указанных логических заключений следует вывод: что, если форма корпуса корабля плохо оптимизирована по волнообразованию на всех диапазонах скоростей хода, то этот корабль обладает также и плохой мореходностью в условиях реального морского волнения.
Описание корабельного волнообразования
По физическому смыслу функция:
 (19)
(19)
определяет потенциал плоской волны, которую мы можем наблюдать на некотором удалении от единичного источника. Так как амплитудным множителем перед G**
стоит малая величина dΩ, то для подынтегральной функции эти волны можно считать малыми.
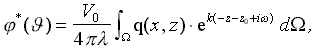 (20)
(20)
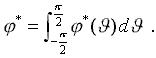
Потенциал φ*(φ) описывает волны конечной амплитуды, так как для его получения ведется интегрирование по всей поверхности корпуса (20).
Рассмотрим механизм сложения корабельных волн, стационарных относительно движущегося корабля и имеющих заданную частоту формы.

Рис. 10. Две системы расходящихся от корпуса корабельных волн: 1-я имеет фазовые характеристики, с частотой формы k=f (φ ); 2-я система волн формируется при их преобразовании к групповой структуре. (1) Положение фронтов волн, имеющих фазовую структуру и движущихся со скоростью V=V0
cosφ; (2) Положение фронтов расходящейся системы корабельных волн конечной амплитуды, полученных сложением элементарных волн от всех участков обшивки корпуса и распространяющихся с групповой скоростью для пакетов волн на глубокой воде; (3) Выделенные полосы на поверхности жидкости, в которых существуют пакеты волн с данной фазовой частотой формы; (4) Отметка волновой поверхности на диаметральной плоскости корпуса корабля; (5) Направление, по которому наблюдается распространение фазовых профилей волн.
Для получения реальной картины корабельного волнообразования необходимо учитывать, что излучаемые корпусом корабля волны объединяются в пакеты, которые движутся с групповой скоростью Vg=1/2 V. При восстановлении волнового поля необходимо производить сложение пакетов волн во всем спектре частот:

Рассмотрим поле скоростей в плоскости распространения фазовых волн. Пусть излучение ведется только с одной площадки на поверхности корпуса, тогда:
 (21.1)
(21.1)
 (21.2)
(21.2)
Аналогичный результат будет получен дифференцированием по времени положения частиц жидкости заданных формулами (15) и (16):
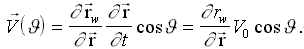 2
2
Здесь учтено, что выражение (15) определяет отклонение частиц жидкости от невозмущенного состояния, в проекции на плоскость { x : z }, в системе координат, связанной с подвижным корпусом.
Как известно [Шебалов, 1984, Егоров, 1974], формулы для описания траекторий частиц жидкости (21.1,21.2), являются также определениями для плоских трохоидальных волн конечной амплитуды, которые иногда называют волнами Герстнера. Это справедливо, если считать V как локальную скорость частицы жидкости в Лагранжевом представлении течения.
Основные свойства волнового поля
Рассмотрим основные свойства корабельного волнообразования на основе полученного поля скорости.
1. Частицы жидкости участвуют в движении по круговым траекториям [Войткунский Я.И., 1982] со скоростью, зависящей от аппликаты z:
 (22.1)
(22.1)
Угловая скорость: 
Локальный радиус траектории: 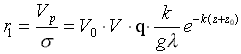 (22.2)
(22.2)
2. Пользуясь условием стационарности рассматриваемого потока жидкости, учтем, что линии тока и траектории частиц совпадают. При переходе же к Лагранжевым координатам, где всегда рассматриваются траектории частиц жидкости, ранее полученные уравнения (21) будут относиться также и к трохоидальным волнам Герстнера.
Подмена кинематической системы отсчета никак не отражается на использовании предположений о линейности волновых свойств потока, по крайней мере в пределах малых частиц жидкости, а сохраняя неизменным дисперсионное соотношение s 2 = g·k, соответственно сохранится и большинство выводов из линейной теории волн (волн на свободной поверхности под действием сил гравитационной природы). Как показано в работе А.Н. Шебалова [1984], такое трактование поля скорости (21) делает его вихревым:
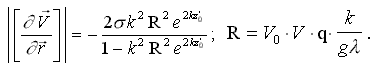
Знак завихренности говорит о том, что в случае вязкой жидкости волны конечной амплитуды (волны Герстнера) будут угасать со скоростью, пропорциональной квадрату амплитуды.
Для получения волновой поверхности и поиска максимальной амплитуды волны в функции от ее «частоты формы» запишем выражение для радиусов траекторий частиц жидкости
(16) в следующем виде: 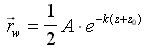 . В соответствии с трохоидальной теорией, локальная траектория частиц жидкости описывается дугой окружности с радиусом rw, зависящим от текущей аппликаты: z, для данной частицы жидкости zw и от амплитуды волны на поверхности:
. В соответствии с трохоидальной теорией, локальная траектория частиц жидкости описывается дугой окружности с радиусом rw, зависящим от текущей аппликаты: z, для данной частицы жидкости zw и от амплитуды волны на поверхности:
 . Скорость движения элементарных частиц определяется через произведение частоты колебаний и радиуса дуги траектории:
. Скорость движения элементарных частиц определяется через произведение частоты колебаний и радиуса дуги траектории:
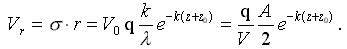
Скорость движения частиц жидкости возрастает с уменьшением глубины z. На вершине волны эти частицы перемещаются с максимальной скоростью в направлении движения ее гребня.
Допустим, что скорость частиц жидкости не должна превышать скорости распространения корабельной волны, так как это является условием разрушения волнового гребня. В этом случае максимальная скорость V=Vr :

В предельном случае трохоидальная теория, путем численного (приближенного) решения полученного соотношения, дает константу: A·k
» 1.134, при: z = A /2, или с учетом снижения амплитуды на подошве волны получается: λ/h »
8.38, что соответствует прогрессивной волне с интенсивно разрушающимся гребнем.
Полученное соотношение определяет весьма важное свойство волн Герстнера, как реальных вихревых волн конечной амплитуды, и должно быть использовано при физической интерпретации характера волнообразования от всего корпуса корабля.
Формула Мичелла для волнового сопротивления
При построении формулы для волнового сопротивления корабля на основе линейной теории волн, которая подразумевает существование потенциалов (2’): Ф = -V0x + φ0 +φ*, будем пользоваться потенциалом G** (19), который описывает малые возмущения, вносимые в поток с элементарной площадки на поверхности корпуса: dΩ. Основываясь на энергетических зависимостях линейной теории волн, определим энергию, распределенную по взволнованной поверхности моря, которая приходится на образование одной волны с длиной l:
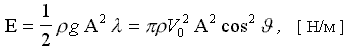 (23)
(23)
Далее учтем, что скорость переноса энергии определяется через групповую скорость пакета, состоящего из фазовых волн: 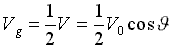 (для глубокой воды). Излучение корабельных волн ведется в диапазоне:
(для глубокой воды). Излучение корабельных волн ведется в диапазоне: 

Рис. 11. Картина корабельного волнообразования обладает свойством неподвижности относительно идущего с постоянной скоростью корабля, при этом поперечные волны в следе корабля обладают строгой регулярностью, а ограничивающие их расходящиеся волны имеют ярко выраженную групповую структуру с обрушающимися гребнями и частично стоячими фронтами одиночных волн. |
Из условия стационарности картины волнообразования относительно движущегося корабля следует, что фазовые профили всех излучаемых волн отображаются на диаметральную плоскость корпуса как волны одинаковой длины. Это означает также, что пакеты волн любой частоты содержат одинаковое количество периодов фазовых волн, в точности укладывающихся на волнообразующую длину корпуса.
Мощность, затрачиваемая кораблем на образование волн, излучаемых в направлении ÐJ , выражается следующим уравнением:
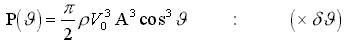 (24)
(24)
Волновое сопротивление от всего спектра корабельных волн:
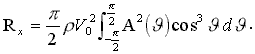 (25)
(25)
Полученный интеграл иногда называют формулой Хавелока [Ньюмен, 1985]. Амплитудную функцию A(φ ) можно получить из линейного граничного условия на свободной поверхности жидкости (7), применяя его к выражению для потенциала от всего корпуса (20), подобно тому, как это делалось при получении формул для линий тока и аппликат частиц жидкости (16) и (17).
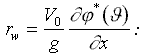 (7) Þ (20)
(7) Þ (20)
 (16) Þ (17)
(16) Þ (17)
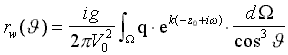 (26)
(26)
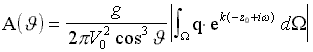 (27)
(27)
После подстановки амплитудной функции (27) в формулу Хавелока (25) может быть получен аналог интеграла Мичелла, который по сути является точной копией выражений, связанных с именем Н.Е. Кочина.
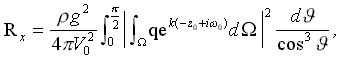 (28)
(28)
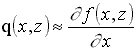 ; Ω0 = x0 cosφ по Мичеллу): Ω0 = x0 cosφ + y0 sinφ (по Кочину).
; Ω0 = x0 cosφ по Мичеллу): Ω0 = x0 cosφ + y0 sinφ (по Кочину).
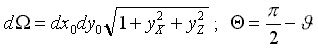 - угол фронта. 3
- угол фронта. 3

Рис. 12. Распространение и интерференция фазовых волн. (1) Точка, в которой невозможно излучение носовой расходящейся волны с данной фазовой частотой; (2) Точка, в которой корабельная волна отрывается от корпуса, до этой точки волны заданной частоты складываются в гребень; (3) Точка, в которой нарушается условие отхода кормовой расходящейся волны; (4) Линия, задающая направление распространения плоских фазовых волн, вдоль которой происходит интерференция этих волновых движений; (5) Фронт расходящейся корабельной волны с данной фазовой частотой.
Переходя к физической и геометрической интерпретации полученных формул, сделаем повторение выкладок для получения амплитудной зависимости (27), но уже с помощью геометрических построений на основе потенциала G**. Это позволит выявить области с нарушениями физических законов реального волнообразования, которые допускаются в случае прямого интегрирования формулы для вычисления волнового сопротивления корабля (28).
Используем описание волнового поля в связанной с корпусом системе координат (16): . Амплитуда волны на свободной поверхности жидкости (z=0), полученная в результате излучения с единичной площадки на обшивке корпуса, представляется как:
. Амплитуда волны на свободной поверхности жидкости (z=0), полученная в результате излучения с единичной площадки на обшивке корпуса, представляется как:
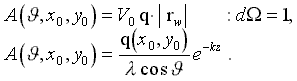 (29)
(29)
Допустим, что каждый элемент обшивки корпуса создает на свободной поверхности жидкости приращение амплитуды корабельной волны, фронт которой простирается вдоль линии, обозначенной на рис. 11 символом: … при этом фаза волны не меняется вдоль фронта, а амплитуда вычисляется по формуле (29). Поставим точки на линии`w ’: „ в соответствие с точками на поверхности корпуса:
`w ’ = x0 cosφ + y0 sinφ, (30)
где учтено, что вектор `w ’ может перемещаться вдоль фронта фазовой волны, а в формуле (30) он проведен из начала координат: ( x=0, y=0 ).
Тогда, записывая результирующую амплитудную функцию для фазовых волн, как результат их интерференции на линии`w ’:
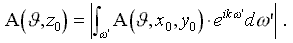 (31)
(31)
Интегрирование вдоль вектора`w ’ усложняется тем, что направление`w ’ задается фазовым углом φ . Воспользуемся тем свойством, что из условия стационарности картины волнообразования любая система фазовых волн единообразно проектируется на направление движения корабля. Тогда можно поменять параметр интегрирования dΩ на dx, и при этом пересчет w ‘ под экспонентой в формуле (30), будет правильно определять фазу волны в интерференционном интеграле (31).
 (32)
(32)
Амплитудная функция от всего корпуса:
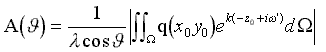 (33)
(33)

Из геометрического построения формулы (33) можно отметить отсутствие корректности при включении в интерференцию волн, излучаемых с участка корпуса от форштевня до точки ‚ и ѓ от точки до ахтерштевня (по рис.11). Получение же аналогичной формулы из волнообразующего потенциала: φ*(φ ), ввиду формальности преобразований (7) Þ (20)Þ
(26)Þ (27), полностью исключает этот вопрос из рассмотрения.
Для уточнения расчетов волнового сопротивления корабля, которые будут выполняться с использованием уравнений, полученных на основе линейной теории волн, необходимо продолжить геометрическую и физическую интерпретацию формул для волнового сопротивления корабля (28) и корабельного волнообразования (33).
Вычислительная модель на основе интеграла Мичелла
Для решения этой задачи все математические выкладки выполнены в физически значимых переменных, допускающих размерное представление расчетных величин, и соответственно физическое и геометрическое понимание сути всех вычислительных объектов и операций. В результате подынтегральное выражение было определено с помощью амплитуды корабельной волны, источники излучения которой локализуются до элементарных участков судовой обшивки:
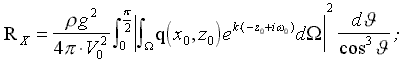 (28’)
(28’)
или:  (25’)
(25’)
и:  (33’)
(33’)
где: 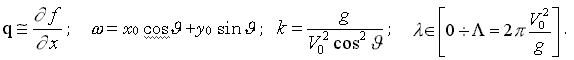
Новый интеграл Мичелла описывает трансформацию падающих на корпус волн в диапазоне длин λ от 0 до λ, при этом волнообразование рассматривается как своеобразная деформация внешних морских волн в процессе их отражения от корпуса. Принятие такого объяснения корабельного волнообразования соответствует выводу о том, что
минимизация волнового сопротивления на всех скоростях хода одновременно минимизирует силовое воздействие на корабль со стороны штормового волнения.
Непосредственное использование для расчетов волнового сопротивления корабля формул, полученных в предыдущей главе, сопряжено с рядом трудностей, в том числе связанных с их формальными недостатками. При построении численных решений очень важно учитывать и по возможности корректировать недостатки интегралов Мичелла, обусловленные использованием линейной теории волн, что реально, исходя из анализа и геометрической интерпретации картины волнообразования, а также привлечением к эмпирическим аппроксимациям свойств волн Герстнера как реальных морских волн конечной амплитуды.
При получении формулы для волнового сопротивления (25) использовалась линейная теория волн, на основе которой можно делать выводы для гравитационных волн заведомо малой амплитуды. Имеется в виду случай, когда амплитуда существенно мала по отношению к длине волны, что формально позволяет не разделять траектории и линии тока, которые, в том случае, сводятся к простым гармоническим функциями вида: ek·(-zo+iΩo).
Оценка энергии волнообразования: E = r·g·A2 / 2. (34)
В основу энергетической зависимости (34) закладывалось допущение о том, что с элементарной площадки на поверхности корпуса корабля излучаются “малые волны”. Но амплитудная функция А(φ) (33) описывает волнообразование от всего корпуса, т.е. А(φ) определяет реальные корабельные волны с большой амплитудой, и более того при J® p /2Þ A® ¥.
Второй способ получения амплитудной функции основывается на геометрических построениях с целью получения общей картины волнообразования, где используется суммирование фазовых волн и их групповых пакетов. Фазовые волны образуют систему расходящихся корабельных волн, в которой скорость убегания волн от корпуса зависит от длины волны, определяемой углом φ.
Справедливость формальных математических преобразований, при получении амплитудных зависимостей А(φ), может быть подвергнута сомнению для участков корпуса вблизи оконечностей, где скорость поперечных перемещений жидкости, вызванная поступательным движением корпуса, превышает скорость распространения корабельных волн с высокой частотой φ. В этой области в носовой оконечности корпуса происходит образование разрушающегося гребня, который нельзя описать с помощью волновых уравнений. Такие участки корабельного корпуса характеризуются активной зависимостью волнообразующих источников от поля потенциального обтекания корпуса и некорректностью применения аддитивного разложение типа: Ф = -V0x + φ0 + φ*.
В то же время в рассуждениях неявно применялось правило отражения круговой волны от единичного источника, расположенного на поверхности корпуса. Для формирования корабельной волны, излучаемой всем корпусом корабля, использовалось простое интегрирование (сложение) всех источников, распределенных по поверхности корпуса. Но к потокам вблизи корпуса судна нельзя применять анализ волнообразования в потенциалах, так как здесь потенциал обтекания корпуса φо не удовлетворяет динамическому граничному условию на поверхности взволнованной жидкости, с заведомо большой амплитудой волн, а волновой потенциал φ* соответственно не участвует в выполнении условий непротекания на поверхности корпуса.
Для получения адекватной вычислительной модели корабельного волнообразования необходимо отказаться от применения аддитивного разложения и соответственно не попытаться в точности удовлетворить все граничные условия вблизи корпуса. Очевидно, что в настоящее время невозможно построить строгого решения с помощью потенциалов или математического аппарата скалярных функций векторного аргумента, а соответствующие вычислительные модели векторных полей векторного аргумента еще только разрабатываются.
Вблизи корпуса движущегося корабля происходит интенсивное вихреобразование, в процессе которого формируются свободные трохоидальные волны конечной амплитуды. Нельзя ли с помощью вихревой энергетики попытаться определить явления, связанные с разрушением гребней волн в непосредственной близости от корпуса, а также в районах пересечения гребней расходящейся и поперечной системы корабельных волн?
Для практической интерпретации вычислений по формулам (25) и (33) воспользуемся геометрическими свойствами трохоидальных волн Герстнера с целью поиска системы эвристических правил для пересчета характеристик волн, имеющих большую частоту формы, чем:  , то есть тех волн, которые не могут оторваться от корпуса.
, то есть тех волн, которые не могут оторваться от корпуса.
Условие образования свободных волн
Волна не может отойти от поверхности корпуса, если ее скорость:
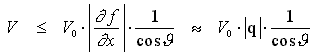 (35)
(35)
меньше, чем скорость движения элемента обшивки корпуса в том же (поперечном) направлении, относительно неподвижной жидкости.
Если корабельная волна не образует фронта плоской поверхностной волны, то она не может быть представлена с помощью потенциала G** (19), теоретически только такая волна может перемещаться на большие расстояния без угасания. Для объяснения условия (35) снова воспользуемся геометрическими построениями для волн, образованных потенциалом G**, задающим излучение с единичной площадки на поверхности корпуса.
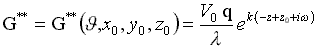 (36)
(36)
Величина V0·q = Q( x0, y0, z0 ) определяет амплитуду поверхностных волн, поэтому можно положить V0
q = 1, так как такое упрощение не нарушает волновых свойств потенциала G** как единичного волнообразующего источника.
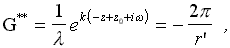 (37)
(37)
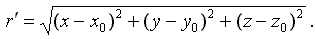
Рассмотрим действие потенциала G** как ориентированного вверх диполя, который образован стоком и источником в точках {zo} и {z}, соответственно. Пусть этот диполь будет расположен вблизи точки { z » zo = 0, x = xo, y = yo }.
G** стремится к образованию на свободной поверхности жидкости кругового купола, по горизонтальным касательным к которому располагаются фронты излучаемых волн. Фазовая скорость движения свободных корабельных волн определяется как: V=V0 cos φ, что соответствует движению вдоль нормали к образующей диполь окружности, но с учетом того, что диполь двигается навстречу потоку вблизи свободной поверхности жидкости. Кормовая часть дипольной окружности соответствует интервалу фазовых углов J Î ] ± π/2: ± π ] и образует систему волн, где каждую волну можно представлять как проходящую на противоположный борт сквозь диаметральную плоскость. Последнее можно определить также с помощью понятия отражаемой от корпуса системы внешних волн.
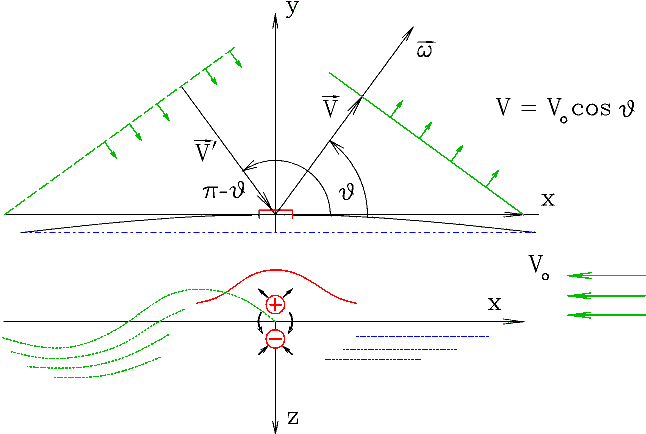
Рис. 13. Действие волнообразующего потенциала G** подобно диполю, который подбрасывает жидкость вверх.
Все сказанное выше можно рассматривать как систему аналитических описаний, относящихся «к тонкому судну Мичелла», и интерпретировать как волнообразование, измеренное на достаточно большом удалении от корпуса корабля. Реальная картина течения и волнообразования вблизи корпуса существенно сложнее, однако теория Мичелла допускает применение эмпирических или специальных асимптотических численных методов, которые могут позволить инженерные решения как для уточненного расчета волнового сопротивления, так и для построения картины корабельного волнообразования и соответственно оптимизации формы корпуса по критерию минимизации энергии излучаемых (трансформируемых) корабельных волн на различных скоростях хода.
По исходной постановке задачи (Ф = -V0x + φ0 +φ*) потенциал φ* действует в потоке, неискаженном влиянием корпуса, где угол падающей внешней волны всегда равен углу отраженной свободной волны. Соответственно первый уровень упрощения задачи должен быть связан с тем, что не учитывается влияние угла входа ватерлиний на направление распространения расходящихся волн. Пренебрегается также эффектом перераспределения амплитуд по направлению излучения корабельных волн (по угловому параметру φ.), обусловленным влиянием реальной ширины корпуса судна.
Тогда:  (38)
(38)
если: 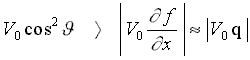
а также: 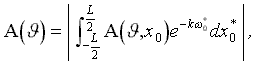 (39)
(39)
в том случае, если: V0 cos2J < | V0 q |.
Здесь x* отсчитывается по потоку от форштевня до точки A, в которой происходит отрыв расходящейся волны от корпуса, а также от аналогичной точки в корме B и до ахтерштевня.
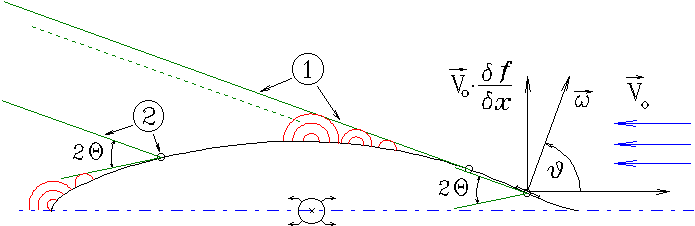
Рис. 14. Геометрическая интерпретация условий формирования фронта расходящейся волны.(1) Условием формирования корабельной волны является сложение амплитуд волновых импульсов, излучаемых одновременно из различных точек обшивки корабельного корпуса; (2) Волна с заданной «частотой формы» не может быть сформирована, если касательная к поверхности корпуса не попадает в сектор 2·Q.
Искусственно сконструированный интеграл (39) производит сложение волн, образующихся в районе оконечностей, в отличие от исходного интеграла (38),
который определяет процесс интерференции корабельных волн, образующихся вдоль корпуса. Экспонента под интегралом учитывает, что амплитуда, являющаяся функцией от фазового угла или частоты формы (A(φ)=A*(k)), не может расти до бесконечности, и по мере возрастания величины амплитуды уменьшается скорость ее роста.
Вывод формулы (39) основывается также на том, что в случае нарушения условий отхода волны от поверхности корпуса, должен изменяться знак в базовом дифференциальном уравнении, которое описывает волновые движения жидкости. В нашем случае можно воспользоваться другим частным решением для плоской волны [Войткунский Я.И., 1982]. Функция для потенциала G** примет вид:
 (40)
(40)
Переход же к формуле (39) осуществляется только при следующих допущениях:
- частота формы волны k не меняет величины в оконечностях корпуса, где нарушены условия отхода фазовой волны от корпуса;
- потенциал G’ применим только на свободной поверхности, где z=0;
- амплитуда рассчитывается по старым формулам, независимо от условий (35):
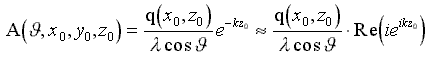 (41)
(41)
Группировка волн в разрушающиеся гребни
Мгновенная амплитуда в точке вершины волны не может превышать величины A<1.134 / k, а высота волны должна удовлетворять ограничению:
h£ 0.75 / k или h£ l /8.38£ 1. (42)
Если же крутизна волны превышает эти ограничения, то происходит интенсивное разрушение гребня волны с образованием буруна на ее вершине [Павленко, 1953], что качественно изменяет расчетную модель волнообразования.
При численном построении картины волнообразования и выполнении расчетов волнового сопротивления возможно использование двух способов ограничения роста амплитуды, в зависимости от выполнения условия (35): V·cosJ £ V0q.
1. Если условие (35) выполнено и расчеты ведутся по формуле (38), то необходимо искусственно ограничивать амплитуду волнообразования:
A(φ,x) = òA(φ,x,z)·e-kz dz, (43)
каким-то из искусственных способов добиваясь, чтобы амплитуда была не выше чем: A(φ ,x) £ 1/ k .Таким образом, из расчетов будет исключаться энергия разрушающихся гребней, которая в случае безусловного использования линейной теории волн может необоснованно накапливаться. При построении картины волнообразования такие эффекты проявляются большими амплитудами волн и их завышенной крутизной.
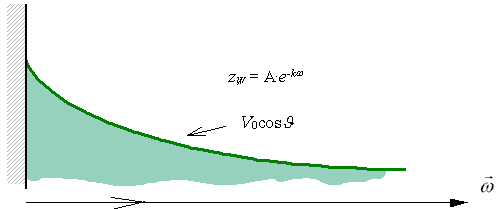
Рис. 15. Формирование волнового гребня в районе форштевня.
2. Если же условие (35) не выполнено, то это означает, что волна не может оторваться от корпуса. Здесь можно применить метод накопления объема жидкости в зоне образования гребня, когда в соответствии с ростом амплитуды волны будет изменяться частота формы волны k. При этом должна поддерживаться постоянной площадь сечения под линией, задающей подъем свободной поверхности перед корпусом в направлении вектора `w (φ ).
Площадь под кривой ZW=A·e–kΩ определяется интенсивностью волнообразующих источников q(x0, y0, z0), которые распределены по поверхности корпуса. Допустим, что Ao получается в результате расчетов амплитуды по формуле (9); ko
- используемая в расчете частота формы излучаемой волны должна удовлетворять следующему условию: 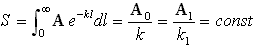 . Новая амплитуда волнового гребня и связанная с ним частота формы волны могут быть согласованы с условием отсутствия обрушения гребня стоячей волны:
. Новая амплитуда волнового гребня и связанная с ним частота формы волны могут быть согласованы с условием отсутствия обрушения гребня стоячей волны:
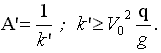 (45)
(45)
В результате: 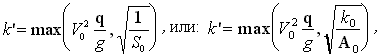 (46)
(46)

Рис. 16. Вблизи корпуса корабля происходит интегрирование и усреднение энергии всех высокочастотных проявлений корабельного волнообразования, с последующим излучением только некомпенсированной волновой энергии. |
В формуле (46) уже учтено, что если при уменьшении k перестанет выполняться условие отхода волны от корпуса (35) cos2J < | q |, то амплитуда волны должна быть ограничена максимумом для стоячих трохоидальных волн. По-видимому, превышение амплитуды должно быть исключено из расчетов, так чрезмерное заострение гребня обычно сопровождается его разрушением, которое пока будем исключать из общей картины волнообразования.
Формула (46) моделирует процесс стекания жидкости с гребня присоединенной к корпусу волны, такое стекание обычно наблюдается в эксперименте. В результате происходит уменьшение частоты формы волны, что проявляется как увеличение длины волны в точке ее отрыва от поверхности корпуса.
Для корпуса с полными обводами нарушение условия (45):  может привести к нарушению стационарности картины волнообразования, что обычно наблюдается в опытовых экспериментах и объясняется свойствами потенциала (40)
может привести к нарушению стационарности картины волнообразования, что обычно наблюдается в опытовых экспериментах и объясняется свойствами потенциала (40) 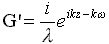 , допускающего осцилляционные решения также и в направлении аппликаты z.
, допускающего осцилляционные решения также и в направлении аппликаты z.
В заключение необходимо отметить, что приведенные выше рассуждения и математические выкладки сделаны не только для обоснования расчетов волнового сопротивления. Это не имело бы особого значения в работе, посвященной проектированию мореходной формы корпуса корабля. Полученные уравнения и выводы могут быть использованы с целью восстановления поля корабельного волнообразования за движущимся кораблем, в котором каждый волновой гребень будет зависеть от формы конкретных участков поверхности корпуса. Возможность построения таких волновых полей необходима в качестве инструмента при проектировании формы корпуса корабля, приспособленного к плаванию как на спокойной воде, так и в условиях штормового волнения.
Математическая оптимизация подводных обводов и надводной формы корпуса корабля, по сути, является поиском технических решений, обеспечивающих прохождение штормовой волны через корпус с минимальными искажениями. Однако аналогичные математические модели описывают отражательные свойства формы корпуса под воздействием гидроакустических или радиолокационных волн, откуда следует дополнительное предположение, что оптимизация штормовой мореходности способствует скрытности корабля в море, а исторические корабли начала XX века удовлетворяли требованиям современных стеллс-технологий.
Численная реализация расчетов волнового сопротивления
Для более ясного понимания вычислительных алгоритмов и применения эмпирических зависимостей при невозможности прямого численного решения интеграла Мичелла (25’,33) имеет смысл заменить аргумент в виде фазового угла Кельвина φ на длину излучаемой корпусом корабельной волны l :
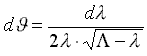 – выражение для дифференциала;
– выражение для дифференциала; 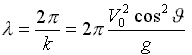 – фазовая длина волны; L=2pV02/g
– критическая или максимальная длина поперечной волны;
– фазовая длина волны; L=2pV02/g
– критическая или максимальная длина поперечной волны;  – аналог волнового число Маха; C=V0 /M – фазовая скорость волны;
H=A·l·M/4 – функция Кочина. Тогда основные расчетные формулы примут вид:
– аналог волнового число Маха; C=V0 /M – фазовая скорость волны;
H=A·l·M/4 – функция Кочина. Тогда основные расчетные формулы примут вид: 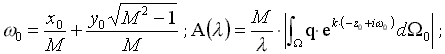
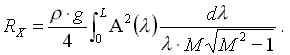
В общем случае функция A(λ) сильно осциллирует и имеет особенность порядка λ- 3/2 при l® 0. Интеграл (14) для вычисления волнового сопротивления имеет особенности на границах порядка λ-1/2 при
l® 0 и l® L.
Указанные особенности могут быть ослаблены при использовании условий, учитывающих особенности волнообразования вблизи поверхности корпуса. Эти особенности обсуждались в предыдущей главе (формулы 35, 38, 39, 42 и 46 ).
Интеграл по ватерлиниям
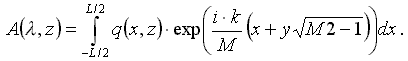 (47)
(47)
При малых значениях λ интеграл сильно осциллирует, в то же время при λ, имеющей порядок длины корпуса, этот интеграл не представляет никаких особенностей и может быть вычислен по методу Симпсона (“трапеций”). Для оценки степени осцилляции вводится параметр Np, задающий минимальное количество расчетных точек на одну длину волны λ . Критерием допустимости прямого интегрирования может быть поставлено следующее условие: где L - длина между перпендикулярами; Ni - количество шпангоутов; Np - допустимое количество точек аппроксимации, приходящихся на один период рассчитываемой корабельной волны.
где L - длина между перпендикулярами; Ni - количество шпангоутов; Np - допустимое количество точек аппроксимации, приходящихся на один период рассчитываемой корабельной волны.
В случае если условие (17) не выполняется, то можно воспользоваться линейными аппроксимациями подынтегральных функций и аналитическим интегрированием каждой шпации в отдельности.
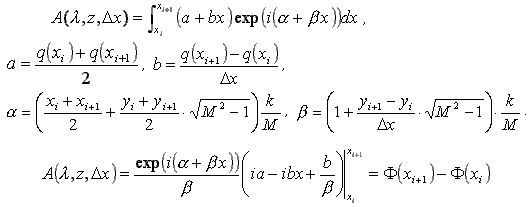
Абсолютное значение интеграла А(λ,z) всегда меньше, чем максимальное значение по абсолютной величине от подынтегральной функции, равное максимуму от
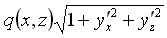 , достигаемому вблизи штевней. Если заранее рассчитать такие максимумы, то критерием достижения заданной точности при вычислении интеграла по ватерлиниям явится выражение e-kz| max(q·Ω)| > eps.
, достигаемому вблизи штевней. Если заранее рассчитать такие максимумы, то критерием достижения заданной точности при вычислении интеграла по ватерлиниям явится выражение e-kz| max(q·Ω)| > eps.
где eps - принятая в расчетах абсолютная точность.
Иначе А(λ,z) = 0, если e-kz· | max(q·Ω)|> eps.
Интегрирование результатов расчета по ватерлиниям
 (48)
(48)
имеет экспоненциальную особенность при z® 0, которая определяет его величину при больших значениях k (то есть малых
λ ). Так как подынтегральная функция e-kz всегда положительна, то знак абсолютной величины в формуле (13’) может быть перенесен на А(λ,z). Знак абсолютной величины ослабит, но не исключит возможность осцилляции функции А(λ,z), поэтому выбран метод вычислений, суть которого можно определить как двойную аналитическую аппроксимацию А(λ,z) в точках вблизи действующей ватерлинии (где: z®0).
Аппроксимируя |А( λ,z)| = f( z ) с помощью параболы:

где: f’ = f e-bx; f” = f e-bx2.
Ось Z полагается разбитой на равные интервалы: D z – расстояние между ватерлиниями; Z1 =
D z; . Z2 = 2Dz, то:
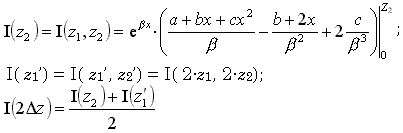
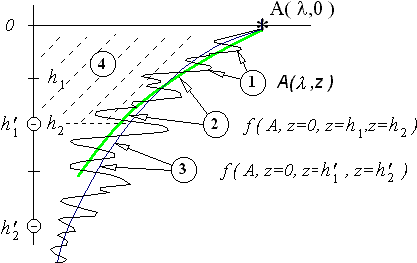
Рис. 17. Геометрическое представление функции А(λ,z) и ее аналитических аппроксимаций.
Показанная аналитическая аппроксимация применяется только в том случае, если значения функции |А( λ,z)| в точках z=0 и z=dz отличаются на порядок. Иначе ведется прямое интегрирование по методу Симпсона.
Если же А(λ,0)/А(l 1,z1)>12, то используется расчет поправки вида:
d А( λ,z) = I( 2dz ) - |А( λ,2 dz)|dz/2
После этого последние две точки в массиве А( λ,zi) обнуляются, и дальнейшее интегрирование ведется по методу трапеций.
Интеграл по волновому спектру, расчет сопротивления
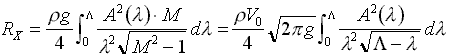 (49)
(49)
Здесь A имеет размерность [м2] и обладает экспоненциальным стремлением к нулю при λ®0. Сам же интеграл имеет особенности в точках l®L типа λ-1/2; l®0 типа
λ-2, которая гасится экспонентой в выражении 
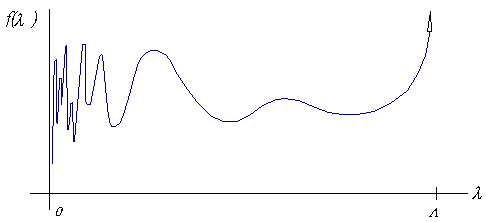
Рис. 18. Характер поведения подынтегральной функции:
При вычислении интеграла по волновому спектру необходимо постоянно оценивать степень осцилляции функции f(λ). Разбивая этот интеграл на две части: 1) [ λi: λ ] - слабо осциллирующую, но обладающую особенностью типа λ-1/2 при l®L; 2) [ 0 : λi
] - сильно осциллирующая часть интеграла.
Для поиска критического значения λi можно воспользоваться следующей оценкой подынтегральной функции в выражении для интеграла по ватерлиниям:
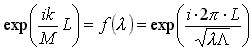 , где: L - длина судна. Если допустить “проход” трех периодов волн в полученной зависимости от аргумента λ, тогда
, где: L - длина судна. Если допустить “проход” трех периодов волн в полученной зависимости от аргумента λ, тогда
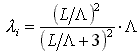 , а отношение λ / L = 2p·FN2.
, а отношение λ / L = 2p·FN2.
Для вычисления интеграла  был использован рекурсивный алгоритм, основанный на использовании полиномов Гаусса 4-й степени, которые удовлетворительно аппроксимируют функции с особенностями на границах интервала интегрирования. При вычислении интеграла
был использован рекурсивный алгоритм, основанный на использовании полиномов Гаусса 4-й степени, которые удовлетворительно аппроксимируют функции с особенностями на границах интервала интегрирования. При вычислении интеграла 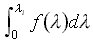 использовался традиционный «метод трапеций», так как его аппроксимации не приводят к разрывам решений с осциллирующими функциями.
использовался традиционный «метод трапеций», так как его аппроксимации не приводят к разрывам решений с осциллирующими функциями.
Математические модели формы корпуса и оценочные расчеты волнового сопротивления
Проведение вычислительного анализа формы корпуса предваряло подготовку к испытаниям модели в опытовом бассейне. С этой целью использовалась математическая модель корпуса, позволяющая варьировать полноту мидель-шпангоута, продольную асимметрию полноты корпуса и размеры носового бульба. Такая модель была создана в 1976 году на борту РТМС "Багратионовск" в Южной Атлантике, чему способствовало наблюдение за штормованием судов океанского рыбопромыслового флота, за необычными мореходными качествами маломерных судов африканских стран, а также, что не менее важно, знакомство с особенностями свободного плавания и активного движения вблизи взволнованной поверхности моря различных животных (рыб, акул, дельфинов и водоплавающих птиц). Эта модель позволила изучить влияние носового бульба, а также получить качественную оценку более сложных элементов несимметричных относительно мидель-шпангоута обводов корпуса.
Для сравнительного анализа волнового сопротивления использовались также традиционные аналитические описания формы корпуса корабля, основанные на применении параболических (степенных) функций, которые при гладком вписывании в контуры штевней в равной мере позволяют оценить главные параметры простейших форм корпуса. Параболическая форма корпуса наиболее ярко отражает особенности корабельного волнообразования, так как при обтекании этих упрощенных корпусов не образуется сложных трехмерных потоков и соответственно не происходит «нелинейной» минимизации волнообразования, что на графиках волнового сопротивления проявляется хорошо выраженными экстремумами на малых скоростях.
Аналитическое описание формы корпуса
Для проведения оценочных расчетов в программное обеспечение были включены две аналитические модели, в которых реализованы возможности задания коэффициентов полноты корпуса и действующей ватерлинии, а также предусмотрено перераспределение подводных объемов вдоль продольной и вертикальной осей. Аналитические модели учитывают изменение главных элементов формы корпуса, которые затем оптимизировались с целью отработки оптимального теоретического чертежа гипотетической модели для экспериментальных исследований мореходности в опытовом бассейне.
Представление формы корпуса для расчетов на ЭВМ
При аналитическом описании формы корпуса возможно получение ординат y(x,z), их производных y’x и y’z, тем не менее, использование этих выражений при выполнении вычислительных экспериментов не всегда удобно. Обычно возникают проблемы, связанные с длительностью вычисления элементарных функций или из-за необходимости унификации описания реальных и модельных корпусов судов.
При проведении численного моделирования волнового сопротивления данные о форме корпуса хранятся в прямоугольных массивах, с помощью которых производится интерполяционное описание отдельных ватерлиний.
Для решения уравнений Мичелла, в которых интегрирование по поверхности корпуса ведется обычно вдоль ватерлиний, каждая ватерлиния может быть разбита на произвольное количество участков (N) в интервале между точками пересечения штевней. При этом расстояние между ватерлиниями может быть произвольным.
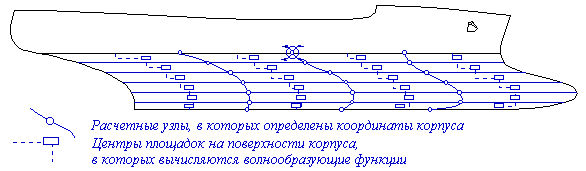
Рис. 19. Дискретное разбиение подводной части судовой обшивки для построения численной модели формы корпуса.
На практике расчеты с использованием сеточного определения формы корпуса выполняются быстрее как при вычислении ординат, так и их производных. Для описания же реального корпуса с целью проведения серии сложных вычислительных экспериментов этот метод является единственным.
Структура основных расчетных массивов в памяти ЭВМ:
FI [ 0:N, 0:K ] - таблица ординат;
YX [ 0:N, 0:K ] - таблица производных f’x;
X [ 0:N, 0:K ] - таблица абсцисс для точек FI;
Z [ 0:K ] - вектор аппликат ватерлиний;
N - количество интервалов разбиения (шпаций) по x (длине корпуса);
K - количество интервалов разбиения по z (слои между ватерлиниями).
“Параболические” (степенные) обводы
При оценке влияния полноты обводов корпуса использовано описание формы корпуса с помощью степенных функций, задающих ватерлинии симметричными относительно мидель-шпангоута.
Построение аналитических обводов корпуса выполняется непосредственно в программе расчета волнового сопротивления по формуле:
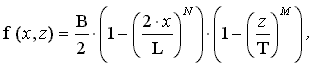
для которой коэффициент полноты площади ватерлинии: α =N/(1-N);
- коэффициент полноты мидель-шпангоута, соответственно: b =M/(1- M)
- и коэффициент общей полноты подводной части корпуса: d = α/b.
Рис. 20. Область определения функций для моделирования параболических обводов формы корпуса.
Целью систематических расчетов волнового сопротивления ставится задача выбора оптимальной формы корпуса для движения на любой скорости хода. В частности на скоростях, соответствующих максимальному волновому сопротивлению при числах Фруда: Fn = 0.3 и Fn = 0.5, а также в области интенсивного излучения расходящихся корабельных волн при минимуме сопротивления на скорости хода: Fn = 0.4
В таких оценочных расчетах волнового сопротивления приняты следующие размерения корпуса: длина – L=90; ширина – B=16; осадка – T=8.
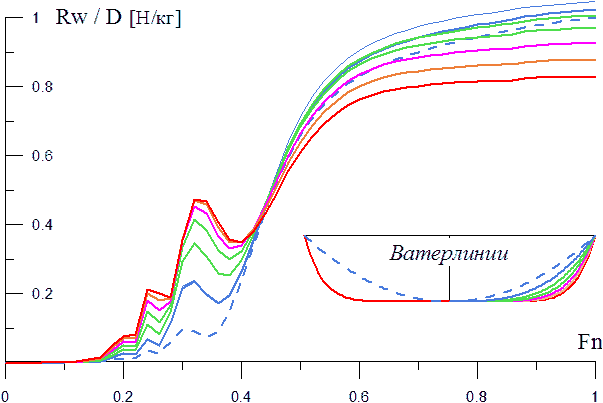
Рис. 21. Расчетные кривые удельного волнового сопротивления, отнесенного к водоизмещению, для симметричного относительно мидель-шпангоута корпуса с параболическими обводами (КПО).
Таблица 1. Основные характеристики расчетных моделей КПО
| N |
M |
α |
b |
S [м2] |
D[м3] |
| 2 |
2 |
0.67 |
0.44 |
2702 |
5120 |
| 3 |
3 |
0.75 |
0.56 |
2940 |
6480 |
| 3 |
4 |
0.75 |
0.6 |
2971 |
6912 |
| 4 |
4 |
0.8 |
0.67 |
3090 |
7373 |
| 5 |
5 |
0.83 |
0.69 |
3190 |
8000 |
| 6 |
6 |
0.85 |
0.73 |
3257 |
8464 |
| 7 |
7 |
0.88 |
0.77 |
3302 |
8820 |
| 8 |
9 |
0.89 |
0.79 |
3333 |
9102 |
Из анализа графиков удельного волнового сопротивления следуют выводы:
- Увеличение полноты ватерлинии существенно сказывается на удельном сопротивлении при скоростях хода Fn = 0.4 и менее;
- Полнота ватерлиний и шпангоутов мало влияет на величину удельного сопротивления при Fn ≥ 0.5, однако при существенном увеличении полноты корпуса удельное сопротивление уменьшается;
- Увеличение полноты мидель-шпангоута приводит к уменьшению удельного сопротивления при скорости Fn = 0.5 и практически не влияет на сопротивление при Fn = 0.3;
- Довольно слабо заметно смещение экстремумов волнового сопротивления вправо, что говорит о том, что волнообразующая длина для обводов корпуса, образованных степенными функциями слабо зависит как от полноты ватерлиний, так и от общей полноты корпуса.
Асимметричный относительно мидель-шпангоута корпус
Построение корпуса основано на произведении косинусоиды с обратной степенной функцией, которые сопрягаются вблизи оконечностей корпуса, где обе функции или их производные терпят разрывы.
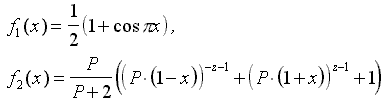
Произведение f1 x f2 образуют семейство кривых, которые в зависимости от параметра P образуют следующие формы ватерлиний:
- Косинусоиды P³10;
- Бульбовые формы ватерлиний 1£P£ 5;
- Форма капли P » 1;
- Форма крыла ската P£0.5.
Из анализа поведения функции f1· f2 вблизи оконечностей сделано заключение, что аргумент z для реального корпуса должен лежать в пределах z Î[0 ¸ 0.5 ], но принятый в расчетах интервал z Î[0¸1] позволяет более контрастно представить особенности формы аналитического корпуса.
Для определения формы мидель-шпангоута введена степенная гипербола: 
которая обеспечивает сохранение формы подводного крыла при малых P и уменьшает полноту мидель-шпангоута до сравнимого с параболой при увеличении параметра
P.
Область определения:
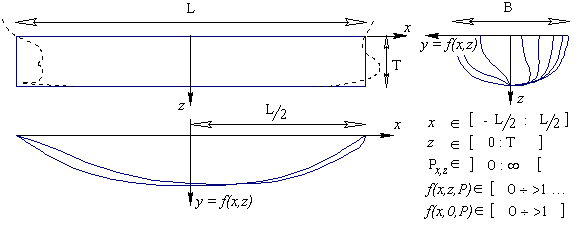
Рис. 22. Система координат и характерные линии асимметричного корпуса.
Можно определить параметры полноты раздельно для кормовой и носовой частей корпуса Pα и Ps:
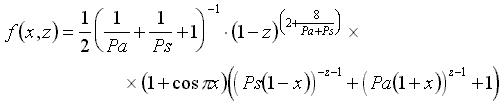
Рис. 23. Кривые водоизмещения (D) и смоченной поверхности (S) в зависимости от параметра P ассиметричной модели корпуса гипотетического судна. L - длина, B - ширина, T - осадка и - объем размерного параллелепипеда.
При этом:
- Увеличение P приводит к заострению ватерлиний в оконечностях и уменьшению размеров бульба, одновременно уменьшается коэффициент общей полноты. При
P®¥, корпус описывается косинусоидами по ватерлиниям и параболами по шпангоутам;
- Уменьшение P приводит к появлению развитого бульба, увеличению глубины погружения и росту его ширины, что может превратить бульб в “крыло ската”. В кормовой части ватерлинии заостряются, превращая ахтерштевень в подобие “плавника”. Увеличивается также и коэффициент общей полноты корпуса, но еще быстрее растет смоченная поверхность;
- Оптимальное соотношение между объемом корпуса и площадью смоченной поверхности достигается при P ≈ 1.5 ( Ch( 1.0 )=1.54308 ).

Рис. 24. Расчетные кривые удельного волнового сопротивления для несимметричного относительно мидель-шпангоута корпуса с экспоненциально-тригонометрическими обводами. Синим пунктиром показан расчет для корпуса с параболическими обводами (КПО), отмеченной под №3 в предыдущей серии расчетов.
Из анализа графиков удельного волнового сопротивления (отношения волнового сопротивления к водоизмещению, рис.24) следуют выводы:
- Применение носового бульба существенно снижает удельное волновое сопротивление на скорости хода, соответствующей минимуму на Fn = 0.3. При этом большая полнота действующей ватерлинии не приводит к значительному увеличению сопротивления, которое наблюдалось у корпусов с симметричными параболическими обводами;
- Если параметр P ≥ 1.5, то сопротивление на скорости Fn = 0.3 становится исчезающе малым. При этом расчетные алгоритмы были нечувствительны к тому, где - в носу или в корме - находится бульб;
- Если P < 1.5, то применение кормового бульба приводит к значительному росту удельного сопротивления на Fn = 0.3. Но при этом оно сравнимо с сопротивлением корпусов с параболическими обводами;
- Корпус с экспоненциально тригонометрическими обводами (КЭТО) показал худшую ходкость на скорости, соответствующей Fn = 0.5, по сравнению с корпусами симметричными относительно мидель-шпангоута (КПО);
- Можно также отметить, что носовой бульб уменьшает относительную разность между экстремумом удельного сопротивления на Fn = 0.3 и минимумом сопротивления на Fn ≈ 0.35.
За оптимальный корпус можно принять обводы с параметром P = 1.0, так как при таком параметре обнаружен минимум удельного волнового сопротивления на скорости хода Fn=0.5. В этом случае в носовой части корпуса располагается довольно развитый и заглубленный бульб.
Моделирование уменьшенной площади ватерлинии
Как уже показывалось в выводах из исторического анализа мореходных качеств, обусловленных формой корпуса судна, улучшение мореходности на волнении достигается за счет завала бортов в средней части корпуса на уровне действующей ватерлинии. Моделирование такого завала бортов и уменьшенной ширины ватерлинии выполнялось путем линейной деформации всего корпуса по закону:
f*(x,z) = f(x,z)·(1+z·(1-k) ),
где: z = z/T, k - коэффициент сужения (деформации) 5 ширины действующей ватерлинии. Если необходимо сохранить коэффициент общей полноты, то при использовании данной формулы необходимо проводить дополнительную корректировку общей ширины корпуса.
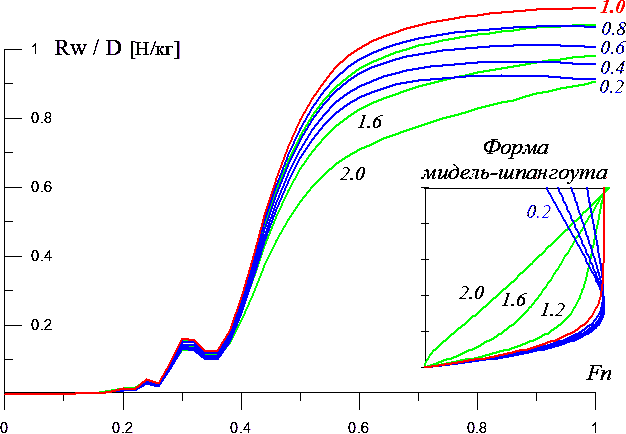
Рис. 25. Расчетные кривые удельного волнового сопротивления при изменении наклона бортов на уровне действующей ватерлинии в средней части корпуса.
Наклон борта в средней части корпуса слабо влияет на удельное сопротивление на малых и средних скоростях хода, до FnЈ0.4. Расчеты также показывают, что обводы с вертикальными бортами дают максимальное волновое сопротивление на больших скоростях при Fn>0.4, когда длина излучаемой корабельной волны становится больше длины корпуса корабля. Как завал, так и развал бортов приводит к уменьшению удельного волнового сопротивления на больших скоростях хода. Это означает, что испытания на спокойной воде в опытовом бассейне, которые редко проводятся на скоростях хода более чем Fn>0.5, могут показать улучшение ходовых качеств как для судна с завалом бортов, так и с его развалом. Реальные испытания штормовой мореходности корабля могут дать обоснованные проектные решения только при постановке соответствующих мореходных испытаний на волнении.
На рисунке показан расчет кривой волнового сопротивления для развала бортов с коэффициентом k=2.0, при котором мидель-шпангоут становится почти треугольным. Несмотря на существенное уменьшение коэффициента общей полноты получившегося корпуса, все же удельное волновое сопротивление на высоких скоростях хода остается достаточно значительным, а это означает, что на такой корпус будут очень активно воздействовать штормовые волны большой длины.
Форштевень
Форштевень описывается с помощью степенных функций, моделирующих заданное положение бульба по глубине ( α ) и определяющих величину выступа этого бульба вперед, от точки пересечения штевнем поверхности воды ( l ).
Область определения:
Рис. 26. Функции, образующие форштевень (а), и результат их произведения (б).
Расчетные формулы для форштевня, образованные произведением двух характерных функций, имеют вид:

где: lÎ ] 0 ÷ 1 [ - относительная длина бульба;
a Î ] 1/2 ÷ 1 [ - относительное погружение бульба.
Важно отметить, что форма корпуса в носовой части корабля отвечает за весь комплекс его мореходных качеств и безопасность мореплавания. Если корабль не может обеспечить движения в штормовую погоду, то его нос должен быть полным, центр величины также должен быть смещен в нос, обеспечивая штормование в режиме гидродинамического флюгера.
Если же речь идет о ходовых качествах корабля, то необходимо помнить не только о минимизации сопротивления “формы” (волнового сопротивления), но и о снижении эффективности взаимодействия корпуса с внешним волнением, для которого требуется отработка обводов как в подводной, так и в надводной частях корпуса.
Это означает, что в носовой части обводов корпуса необходима отработка каждого элемента обшивки корпуса таким образом, чтобы были минимизированы все составляющие корабельного волнообразования, а также отработаны все участки обшивки в надводной части корпуса, которые, потенциально, могут воспринять на себя энергию внешних морских волн.
Ахтерштевень
Задание формы ахтерштевня с помощью сектора эллиптического контура обеспечивает формирование традиционного кормового подзора как для параболической, так и для асимметричной модели корпуса. При этом совсем не обязательно, чтобы ахтерштевень имел именно эллиптическую форму, а связанное с эллиптическим преобразованием смещение ватерлиний определяет в первую очередь общий характер обводов корпуса в кормовой части.
Ахтерштевень описывается эллипсом:
 , где: l - относительная длина кормового подзора.
, где: l - относительная длина кормового подзора.
Область определения:

Рис. 27. Описание кормового подзора с помощью эллипса.
Окончательный вид линии контура ахтерштевня и кормовые ветви ватерлиний должны согласовываться локально, при этом характер линий тока жидкости должен подстраиваться под особенности работы винто-рулевого комплекса и обеспечивать его безотрывное обтекание. Важным критерием при оформлении кормового подзора является ориентация на стабилизацию корпуса на ходу корабля и обеспечение штормовой безопасности при плавании без хода (когда мощности движителей не хватает для активного управления движением корабля).
Примеры построения аналитических корпусов

Рис. 28. Корпус, построенный из “параболических” функций. В табличке приведены параметры, определяющие форму штевней. На графике справа приведены расчетные кривые коэффициента Сх и удельного Rx/D волновых сопротивлений. В таблице слева внизу показаны также дополнительные параметры: Ns - задает плавную стыковку бульбового профиля с основной линией; Nα - определяет угол пересечения ахтерштевня с ватерлинией.
Теоретические чертежи, приведенные в данной главе, были получены для проведения оценочных вычислительных экспериментов с сериями различных судов, где аналитическое описание формы корпуса гарантировало плавное изменение заданных характеристик судовых обводов. Иллюстрации сняты с растрового изображения на графическом терминале ЭВМ.
В качестве главных недостатков для “параболического” и “асимметричного” корпусов можно отметить упрощенное описание скуловых обводов, где с помощью специальных изгибов корпуса должно происходить гашение энергии расходящихся корабельных волн. Формально же, анализ расходящихся корабельных волн выходит за рамки теории «тонкого судна» Мичелла. Формирование этих волн является сугубо трехмерным процессом, связанным с вихреобразованием на поверхности тяжелой жидкости, где вихревые линии вытянуты вдоль корпуса ( правильное построение формы скуловых шпангоутов могло бы уменьшить волнообразование в точке минимума (Fn=0.4) на кривой остаточного сопротивления).
Так как за основу была взята аналитическая модель корпуса судна, то это позволило провести сравнение результатов испытания в опытовом бассейне с сериями численных расчетов волнового сопротивления. Учитывая, что модель корпуса корабля получилась несколько экстраординарной, для выполнения сравнительных анализов с реальными судами было принято решение о совместных испытаниях с моделями, имеющими традиционные обводы.
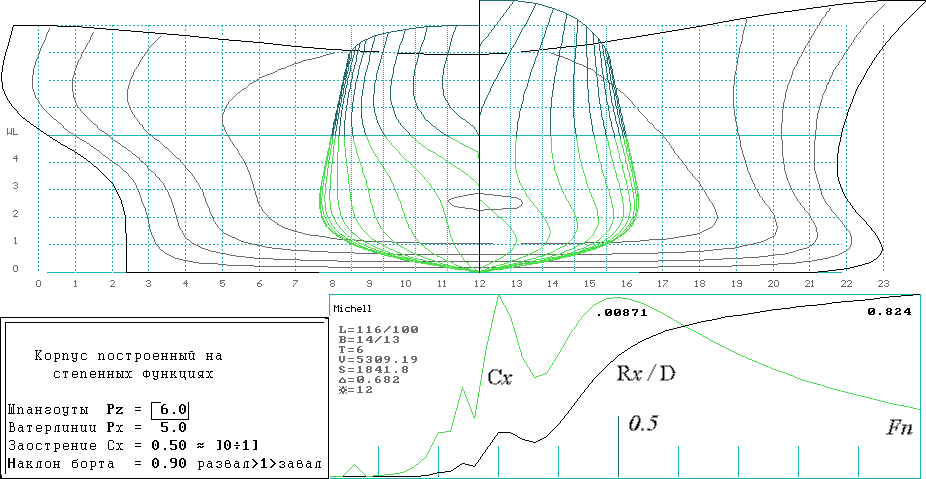
Рис. 29. Тот же корпус, но с увеличенной полнотой ватерлиний, наклонным форштевнем и завалом бортов. Приведены расчетные кривые коэффициента и удельного волнового сопротивления. Хорошо видно, что увеличение полноты ватерлинии приводит к существенному увеличению волнового сопротивления на малых скоростях хода, с появлением ярко выраженного пика на буксировочной кривой на Fn=0.3.
Выбранная модель соответствует случаю усиления мореходных свойств, зависящих от формы корпуса, если в качестве цепочки для сравнения выбрать:
- современный корабль, пассажирское или быстроходное транспортное судно;
- корабль или судно постройки 1920 - 1950 годов;
- корабль или судно, построенное в XIX веке или до 1905 года;
- гипотетическое судно, выбранное для испытаний в опытовом бассейне в 1985 году.
Из анализа следующих рисунков можно понять трудности при оптимизации формы скуловых шпангоутов, так как при уменьшении волнового сопротивления за счет влияния бульба на (Fn=0.3) одновременно наблюдается рост сопротивления за счет сглаживания минимума на скорости, соответствующей (Fn=0.4). Для решения задачи об оптимизации формы корпуса на этих промежуточных скоростях необходимо как уточнение расчетов по формулам Мичелла, путем полуэмпирического учета нелинейных эффектов волнообразования, так и дополнительный анализ волновой картины с целью ее физико-геометрической интерпретации и поиска решений по форме корпуса в районах скулы и кормовой раковины.
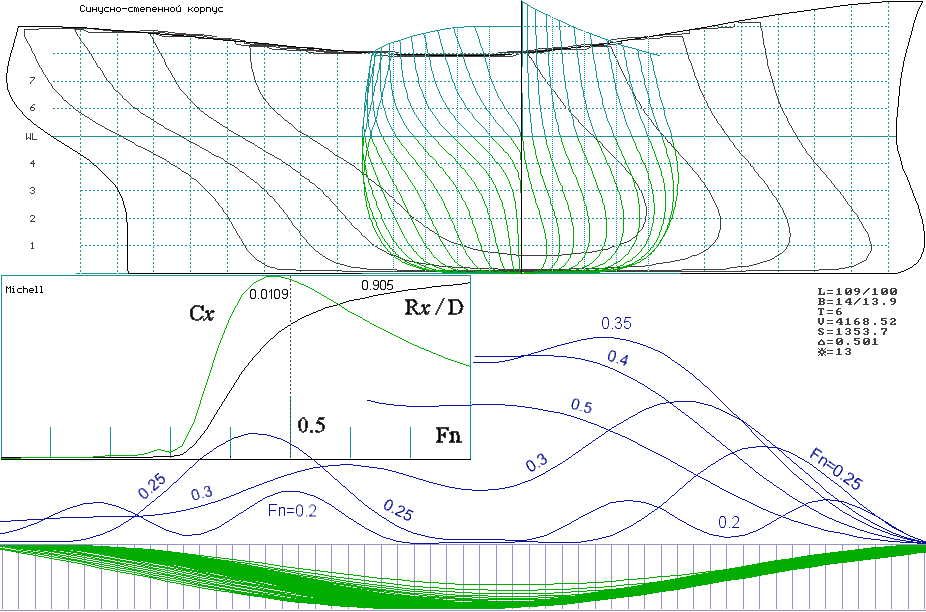
Рис. 30. Асимметричный относительно мидель-шпангоута корпус позволяет минимизировать волновое сопротивление на скоростях хода до чисел Фруда порядка Fn=0.3, чему способствует смещенная в нос полнота подводной части корпуса. Аналогичный выигрыш на средних скоростях хода дают обводы корпуса в виде «двойного клина». При этом, несмотря на очень вогнутые и острые ватерлинии, удельное сопротивление на Fn=0.5 не уменьшилось, а также минимум на Fn=0.4. Синими линиями показано распределение интенсивности зарождающейся вдоль корпуса волновой энергии. Числа рядом с этими кривыми отмечают соответствующую скорость хода.
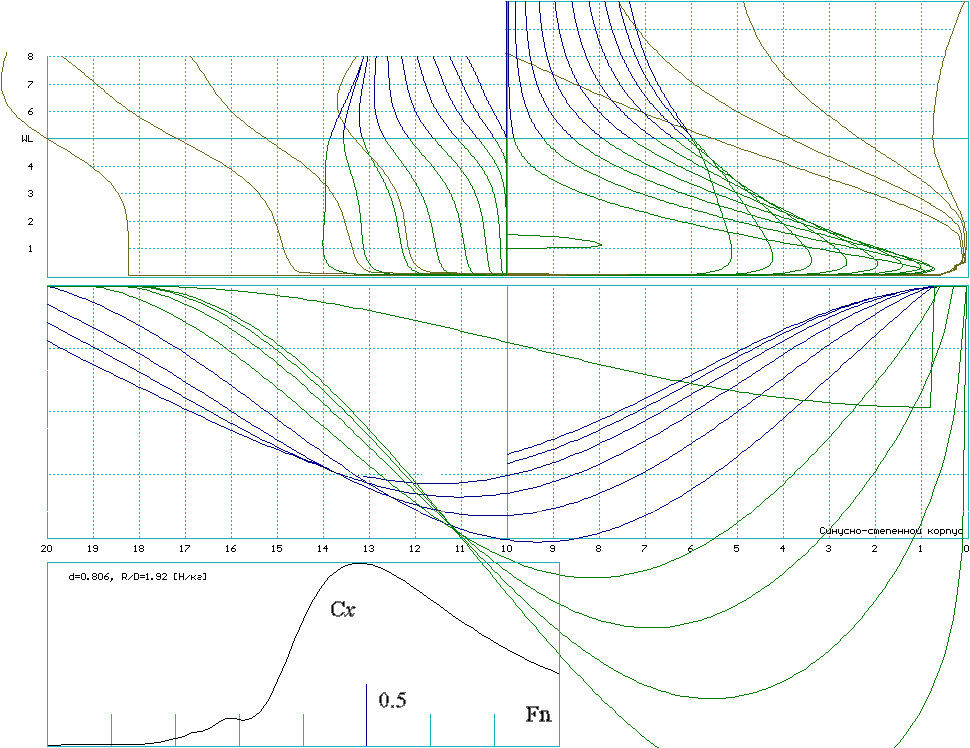
Рис. 31. Крайняя форма аналитического представления бульбовых обводов, когда бульб становится похожим на «крыло ската».
Главной целью настоящего исследования является поиск обобщенных методов снижения волнообразования и взаимодействия корпуса корабля со штормовым волнением. Вычислительные эксперименты поэтому ограничиваются минимизацией поперечной системы корабельных волн, образующихся на больших скоростях хода (в том числе при Fn ≥ 0.5), и которые сопоставляются с силовым воздействием на корабль штормового волнения, когда свободные морские волны соизмеримы или более длинные, чем основные размерения корабельного корпуса. Это позволило несколько упростить вычислительные алгоритмы, использованные в расчетах данной главы (рис. 28-31), справедливость которых обоснована только для скоростей хода более чем Fn ≥ 0,2.
Основные выводы об использовании численных решений
Интегралу Мичелла уже более 100 лет [Michell J.H., 1898], и до настоящего времени он представляется необычайно сложной математической загадкой, неразрешимой в аналитических исследованиях его разрывных и сильно осциллирующих подынтегральных функций и столь же трудной в прикладной постановке численных задач о волновом сопротивлении и корабельном волнообразовании.
Тем не менее, по серии приближенных вычислений можно сделать выводы, что при заострении ватерлиний снижается волновое сопротивление на скорости хода, соответствующей максимуму волнового сопротивления при Fn≈0,3, являющегося барьером ходкости для быстроходных транспортных судов. Подтверждается снижение экстремума на кривой волнового сопротивления на скорости порядка Fn≈0,2, достигаемое применением бульбовых обводов в оконечностях традиционным <закручиванием> скуловых обводов, а также - уменьшением относительной осадки корпуса. При плохом построении формы корпуса, расчеты по Мичеллу предсказывают потерю ходкости в экономичных режимах плавания, соответствующих минимумам волнового сопротивления на числах Фруда порядка Fn≈0,24 и Fn≈0,4.
Реальное поле корабельного волнообразования дает интегральное представление всего спектра излучаемых волн, интерферирующих в условиях эвристических законов Кельвина о групповой структуре свободных трохоидальных волн, что существенно затрудняет поиск геометрических решений по улучшению локальных участков формы корпуса. Потому наиболее эффективным, хотя и трудоемким процессом оптимизации судовых обводов является последовательное рассмотрение профилей вновь зарождающихся и интерферирующих вблизи корпуса корабельных волн определенной длины, выбираемых из всего спектра волнообразования на заданной скорости хода судна. Это позволяет визуально выявлять участки корпуса с аномально высокой амплитудой излучения конкретной корабельной волны, и после локальной деформации формы корпуса, либо снизить местное волнообразование, либо обеспечить интерференционное гашение интенсивности отрывающейся от корпуса волны.
В физической интерпретации интеграла Мичелла обоснована единая природа корабельного волнообразования и силового воздействия на корпус корабля со стороны штормового волнения. В этом случае поиск оптимальной для штормового плавания формы корпуса корабля сводится к минимизации корабельного волнообразования для всех скоростей хода, включая закритически высокие, и для всех посадок (осадки, дифферента и крена), которые судно может принимать в процессе штормовой качки. Тогда оптимальная форма корпуса приобретет веретенообразную форму, с косыми подрезами киля под форштевнем и ахтерштевнем, с обязательным заострением надводных ватерлиний в оконечностях.
Но все же, ко всем расчетным результатам следует относиться очень настороженно, так как теория Мичелла построена на допущениях <узкого судна> с относительно большой осадкой, что формально делает решение двумерным, не учитывающим вертикальных составляющих трехмерных потоков вблизи корпуса корабля. Сложными для расчетов представляются участки корпуса с пологими батоксами, тупыми или бульбовыми ватерлиниями, что требует экспериментальной поверки всех проектных решений о форме корпуса в опытовом бассейне и в свободном плавании самоходной модели различными курсами относительно интенсивного волнения. На экспериментальном этапе должны отрабатываться скуловые обводы корпуса, отвечающие за минимизацию килевой качки и стабилизацию потока в районе движителей; минимизироваться надводные объемы в оконечностях с позиций достижения наилучшей ходкости и безопасности плавания в условиях интенсивного штормового волнения и ураганного ветра; решаться другие вопросы наилучшей мореходности с позиций хорошей морской практики.
Важнейшим фактором, влияющим на форму корпуса и общекорабельную архитектуру, является также технологическая и экономическая обоснованность реализации сложных криволинейных обводов при изготовлении набора и обшивки корпуса. Можно предположить, что отсутствие плоских участков в обводах корпуса положительно скажется на устойчивости бортовой обшивки при ударном воздействии штормовых волн, что в целом приведет к облегчению общей массы корпуса [6].
Вклад науки о мореходности в решение проблем прочности судовых корпусов
Один из величайших российских ученых-кораблестроителей, академик А.Н. Крылов, в «Очерке развития теории корабля», впервые опубликованном в №3 «Вестника Академии наук» за 1945 г. (это было незадолго до смерти ученого), писал о том общем, что всегда требовалось, требуется и будет требоваться от всякого судна: «Это общее – суть мореходные качества корабля: плавучесть, остойчивость, ходкость, плавность и малость размахов качки, поворотливость.» [7]
Практика всегда предъявляла вопросы о том, что и как надо делать, чтобы корабль был крепок и надежен и обладал надлежащими качествами, вместе с тем практика веками, как бы естественным подбором, подходила к решению и этих вопросов, часто весьма своеобразному, как, например, в катамаранах сингалезов и малайцев.
Исследование мореходных качеств корабля, их зависимости от его размеров и соотношений между ними, от формы обводов, распределения грузов и пр. составляет предмет
теории корабля; изучение же его крепости, ее обеспечения правильным, без излишней затраты материала распределением судовых связей составляет предмет строительной механики корабля». А.Н. Крылов в своем обзоре ограничивается рассмотрением теории корабля.
В частности, он указывает, что с 1753 г. Парижская академия наук предлагает на премии целый ряд тем по теории корабля. В этих конкурсах принимают участие Л. Эйлер, братья Бернулли и др.; «разбираются вопросы о нагрузке и распределении грузов на корабле, намечается и дается общая теория напряжений связей корабля как на тихой воде, так и при качке на волнении».
Общие приемы исследования прочности корабля на волнении были даны Эйлером в 1759 г., но лишь в 20-е гг. XIX в. в Англии была разработана рациональная система постройки деревянных судов, учитывающая данные Эйлером представления о действующих на корабль усилиях. Затем в 1870 г. Рид, развив идеи Эйлера и придав им инженерную форму, указал, каким способом при ряде упрощающих допущений следует изучать напряжения в корпусе и рационально распределять материал. Рид рассматривал вопрос статически, не учитывая качки, но затем нетрудно было обобщить его метод и принимать в расчет силы инерции, возникающие при качке.
Заканчивая свой обзор, А.Н. Крылов пишет, что развитие теории корабля шло не чисто умозрительным, отвлеченным путем. Вопросы ставились практикой, обыкновенно какой-нибудь крупной катастрофой с кораблем, на котором не были соблюдены принципы теории. Но и теория должна руководствоваться указаниями практики, согласовывать свои допущения с действительностью, проверять свои выводы опытом и наблюдениями, доставляемыми практикой, работая и развиваясь с нею в полном единении. В этом единении лежит залог правильного развития как теории, так и практики, и перспективы совершенствования корабля.
Волновые нагрузки на корпус корабля
Как известно, существующая в судостроении методика оценки прочности судового корпуса основана на установлении некоторой расчетной нагрузки. По этой нагрузке расчетом определяются напряжения, которые сравниваются с допускаемыми, равными частному от деления опасных напряжений на так называемый коэффициент запаса.

Рис. 32. Типичная схема распределения нагрузок на корпус судна. 1 – силы веса, т/м; 2 – силы поддержания, т/м; 3 - нагрузка, т/м; 4 –перерезывающие силы, т; 5 - изгибающий момент, т·м. |
Если между внешними силами и напряжениями не существует прямой пропорциональности, то расчетная нагрузка умножается на коэффициент запаса, и напряжения сравниваются с опасными. В соответствии с такой методикой расчета в строительной механике корабля различают проблему внешних сил, проблему внутренних сил и проблему проверки прочности [Курдюмов, 1956].
Кроме того, различают общую и местную прочность корпуса. Общая прочность связана преимущественно с общим продольным изгибом корпуса судна как безопорной (свободно плавающей) непризматической балки, загруженной силами собственного веса (самого судна, перевозимого груза, запасов и др.) и силами давления воды (гидростатическими и гидродинамическими). Учет гидродинамических сил требует также введения в рассмотрение сил инерции качающегося судна. При этом бортовая качка не играет заметной роли, тогда как продольная качка весьма существенно влияет на общий продольный изгиб. Общая прочность судна связана с величиной суммарного изгибающего момента, возникающего при плавании на расчетном, наиболее опасном волнении.
Местная прочность относится к отдельным элементам корпуса, которые представляются в виде упрощенных моделей – балок, рам, перекрытий, пластин.
Изгибающие моменты корпуса на волнении>
Со времени И.Г. Бубнова, т.е. вот уже 100 лет, в отечественной практике установилась следующая классификация изгибающих моментов: 1) изгибающий момент на тихой воде, обусловленный несовпадением характера распределения сил веса и сил поддержания на тихой воде; 2) волновой изгибающий момент, связанный с изменением сил поддержания на расчетной волне; 3) суммарный изгибающий момент, являющийся алгебраической суммой первых двух. В зарубежной практике получил распространение несколько иной подход, когда сразу рассчитывался суммарный изгибающий момент, причем при положении судна на вершине волны часть нагрузки (переменные грузы) разносилась в оконечности, а на подошве волны концентрировалась вблизи миделя ([Курдюмов, 1956], c. 19, [Клейтон, 1986], c. 58).


Рис. 33. Транспортное судно на малом ходу встречается с крупной волной на курсе вразрез волне (слева). Развитый носовой бульб подныривает под волну и переносит удар ближе к средней части корпуса, что удерживает нос от резкого всплытия и опрокидывания судна (справа).
Позднее, в связи с аварийными повреждениями корпусов при движении судов с большими скоростями на интенсивном волнении, был введен в рассмотрение ударный изгибающий момент, обусловленный ударами волн в днище в носовой части судна (слеминг). Сравнительно недавно было установлено, что нагрузки значительной величины могут возникать не только вследствие ударов в днище, но и при ударах в развал бортов или в кормовой подзор. При этом сила удара бывает меньше, но его продолжительность – больше, чем при днищевом слеминге. Еще одно явление, которое оказывает влияние на прочность некоторых судов (крупнотоннажных, например, супертанкеров, или длинных низкобортных, например, типа «река-море», или используемых на Великих озерах в США) – это волновая вибрация, называемая за рубежом «спрингинг» (общая вибрация корпуса с частотой первого тона, обусловленная периодически изменяющимися волновыми нагрузками).
В течение длительного времени, примерно до 50-х – 60-х гг. прошлого века, волновой изгибающий момент было принято определять путем так называемой статической постановки на волну. Характеристики расчетной волны выбирались таким образом, чтобы волновой изгибающий момент был наибольшим. Было установлено, что наиболее опасной является волна, длина которой близка к длине судна. Высота расчетной волны зависела от ее длины, вид этой зависимости с течением времени изменялся. Форма профиля волны считалась трохоидальной, что соответствовало теории волн конечной высоты, а вершина или подошва ее совмещалась с миделем.
Предполагалось (см., например, [Курдюмов, 1956], с.44), что статическая постановка на волну физически соответствует случаю, «когда судно идет в направлении бега волны со скоростью, равной скорости волны. В этом случае скорость судна относительно волны будет равна нулю, силы инерции будут отсутствовать, и изгибающий момент может быть определен наиболее просто: этот случай называется статической постановкой судна на волну».
Широкое распространение способ статической постановки судна на волну получил после ряда работ английского кораблестроителя Э. Рида, применявшего его для анализа прочности железных судов. Обоснование выбора особенно опасной волны, вызывающей наибольший дополнительный момент на миделе, было дано только в 1916 г. профессором Петербургского политехнического института А.П. Фан-дер-Флитом в сочинении «Теория корабля», ч. III ([Курдюмов, 1956], с. 46).
А.П. Фан-дер-Флит исследовал величину динамического изгибающего момента на миделе симметричного судна, базируясь на теории килевой качки акад. А.Н. Крылова. Форма ватерлинии принималась параболической: 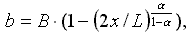 где: L и В – соответственно длина и ширина судна; α - коэффициент полноты ватерлинии.
где: L и В – соответственно длина и ширина судна; α - коэффициент полноты ватерлинии.
В исследовании Фан-дер-Флита изменялись значения α и λ / L, где λ- длина волны. Значения относительных длин волн, для которых были получены максимальные величины волновых изгибающих моментов при условии постоянства высоты волны, приведены в табл. 2, заимствованной из [Короткин, 1965], с. 51. Нетрудно увидеть, что длина наиболее опасной волны постоянной высоты меньше, чем длина судна.
Таблица 2
Зависимость опасной длины волны постоянной высоты от α
| α |
0.50 |
0.67 |
0.8 |
0.9 |
1.0 |
| l/L |
0.67 |
0.72 |
0.80 |
0.84 |
0.89 |
Фан-дер-Флит также получил опасные значения длин волн с учетом изменения высоты h0 согласно зависимости: h0 = λ / 20.
В табл. 3 (см. [Курдюмов, 1956], с. 51) приводятся отношения волновых изгибающих моментов, действующих в миделевом сечении на волнах различной длины, к моменту при длине волны, равной длине судна.
Таблица 3
Относительные изгибающие моменты при переменной высоте волны
| l/L |
α
|
| 0.50 |
0.667 |
0.75 |
0.80 |
0.857 |
0.90 |
1.00 |
| 1/2 |
0.38 |
0.26 |
0.24 |
0.20 |
0.16 |
0.12 |
0 |
| 3/4 |
0.90 |
0.86 |
0.84 |
0.82 |
0.80 |
0.78 |
0.70 |
| 1.0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1.1 |
0.99 |
1.00 |
1.01 |
1.01 |
1.01 |
1.03 |
1.04 |
| 1.2 |
0.97 |
0.98 |
1.00 |
1.00 |
1.00 |
1.02 |
1.05 |
| 1.5 |
0.88 |
0.89 |
0.91 |
0.92 |
0.93 |
0.94 |
1.00 |
Теперь уже наиболее опасная длина волны несколько больше, чем длина судна. Но если принять в качестве расчетной длину, равную длине судна, полученное значение волнового изгибающего момента будет лишь незначительно меньше максимально возможного. Это и является основанием для выбора расчетной длины волны, равной длине судна.
Величина волнового изгибающего момента в миделевом сечении определяется по формуле типа
Mв= kρgrBL2 (50)
где: ρ - массовая плотность воды; g = 9,81 м/с2 – ускорение силы тяжести; r - полувысота расчетной волны; В и L
- ширина и длина судна.
Таблица 4
Коэффициент k в формуле волнового момента
| Автор (год) |
α |
| 0.7 |
0.8 |
0.9 |
| Александер (1905) |
0,0254 |
0,0316 |
0,0396 |
| Шмидт (1909) |
0,0266 |
0,0323 |
0,0400 |
| Суехиро (1912) |
0,0257 |
0,0318 |
0,0393 |
| Фан-дер-Флит (1916) |
0,0253 |
0,0325 |
0,0400 |
| Фостер Кинг (1944) |
0,0267 |
0,0324 |
0,0381 |
| Сваан (1959) |
0,0258 |
0,0323 |
0,0400 |
Входящий в эту формулу коэффициент k при статической постановке на синусоидальную волну зависит от коэффициента полноты ватерлинии
a. Значения k, полученные различными авторами, приведены в табл. 4, заимствованной в [Короткин, 1965], с. 52.
Как видим, разброс значений невелик и не выходит за пределы погрешностей обычных технических расчетов. Обратим внимание на то, что здесь судно считается прямостенным, поэтому абсолютные значения волновых изгибающих моментов на вершине и на подошве волны одинаковы. В действительности при положении судна на подошве волны полнота действующей ватерлинии увеличивается, а на вершине, наоборот, уменьшается, соответственно изменяются и волновые моменты. Я.И. Короткин и А.И. Максимаджи получили следующие значения коэффициентов волнового момента k1 = kρ g для различных коэффициентов полноты ватерлинии ([Короткин, 1965], с. 55):
Таблица 5
Волновые моменты при статической постановке на вершину (k1в)
и подошву (k1п) волны по Короткину и Максимаджи
| α |
0,60 |
0,65 |
0,70 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
| k1в |
0,017 |
0,019 |
0,022 |
0,026 |
0,030 |
0,034 |
0,039 |
0,044 |
| k1п |
-0,025 |
-0,027 |
-0,030 |
-0,033 |
-0,036 |
-0,039 |
-0,043 |
-0,046 |
Таблица 6
Волновые моменты при статической постановке на вершину (k1в) и подошву
(k1п) волны по Мэррею и Манделли
| d |
0.6 |
0.7 |
0.8 |
| k1в |
По Мэррею |
0,0256 |
0,0308 |
0,0360 |
| По Манделли |
0,0259 |
0,0314 |
0,0369 |
| k1п |
По Мэррею |
-0,0292 |
-0,0347 |
-0,0403 |
| По Манделли |
-0,0296 |
-0,0349 |
-0,0405 |
В табл. 6 приведены значения этих же коэффициентов для различных коэффициентов общей полноты судна d, полученные Мэрреем и Манделли ([Короткин, 1965], с. 55). Разница в величинах коэффициентов в табл. 5 и 6 обусловлена несовпадением аргументов (α и d). Отметим, что здесь параметр α является более характерным, чем d.
Характерно, что сумма абсолютных значений (размах) волновых моментов практически не зависит ни от формы профиля волны, ни от непрямостенности обводов судна.
Динамическая постановка корпуса на волну
Модель синусоидального волнения традиционно принимается в расчетах качки; в линейной теории она существенно упрощает решение. При этом форма ватерлинии считается неизменной, т.е. обводы судна принимаются прямостенными. Для полных крупнотоннажных судов такое допущение не приводит к большим погрешностям, но у судов с острыми обводами и пологими батоксами в оконечностях форма действующей ватерлинии на вершине и на подошве волны заметно отличается. При статической постановке на волну качка не учитывается, это дает возможность без существенного усложнения расчетов принимать форму волны трохоидальной, учитывающей конечность ее высоты, в отличие от синусоидальной, соответствующей волнам малой высоты. Здесь также учитывается непрямостенность бортов судна, поскольку расчетная схема предполагает определение входящих в воду и выходящих из воды объемов (двойное интегрирование которых и позволяет рассчитать волновой изгибающий момент) по масштабу Бонжана.
Уравнение трохоидального профиля волны можно записать, придерживаясь А.Н. Крылова, в следующем виде [Короткин, 1965]:
для судна на подошве волны  (51)
(51)
для судна на вершине волны 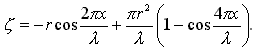 (51a)
(51a)
Постоянное слагаемое p·r 2/λ на величину изгибающего момента не влияет. Таким образом, момент при постановке судна на трохоидальную волну можно представить как сумму (алгебраическую) моментов, получающихся при постановке на две косинусоидальные волны с длинами λ и
λ /2 и амплитудами r и πr 2/λ соответственно. Поправка, учитывающая трохоидальность волны, имеет один и тот же знак на вершине и на подошве волны. Следовательно, на вершине волны при длине волны, равной длине судна, момент на трохоидальной волне будет больше, чем на синусоидальной, а на подошве – наоборот. По данным Сваана, при длине волны, равной длине судна, поправка на трохоидальную форму профиля волны составляет 3%. Обычно считается, что алгебраическая сумма (размах) волновых моментов не зависит от формы профиля волны.
Статическая постановка на волну благодаря своей простоте и наглядности многие годы использовалась для оценки общей прочности корпусов, хотя еще в 1883 г. Смит обратил внимание на то, что за счет орбитального движения частиц жидкости в волне распределение давлений по глубине отличается от гидростатического: сложение сил тяжести и центробежной приводит к тому, что на вершине волны давление уменьшается, а на подошве – увеличивается. Этот эффект легко учесть, вводя вместо действительной высоты (или амплитуды) волны эффективную, которая получается путем умножения на «поправку Смита» k < 1. Величина этой поправки зависит от отношения осадки судна к длине волны T/λ и коэффициента вертикальной остроты судна c = d/a ; ориентировочно можно считать, что для обычного грузового судна при максимальной осадке и длине волны, равной длине судна, эта поправка равна 0,7.
Другой похожий эффект выявляется при несложном анализе уравнений продольной (или только вертикальной) качки судна на регулярном волнении. Он заключается в том, что дифракционные силы инерции, обусловленные отражением волн от корпуса судна, всегда действуют против главной части возмущающей силы, которая носит гидростатический характер и связана с искривлением волновой ватерлинии. Количественно он близок к эффекту Смита.
Характерно, что эти две поправки, которые совместно уменьшают волновой изгибающий момент примерно в два раза, не связаны с качкой. Иначе говоря, если судно будет, не качаясь, двигаться за волной со скоростью волны (именно так принято представлять статическую постановку на волну), то для обычного морского судна возникающий при этом изгибающий момент составит примерно 50 – 65 % от того, который получается при статической постановке на волну ([Короткин, 1965], с.76).
В течение длительного времени влияние качки, по мнению специалистов, сводилось в первую очередь к возникновению сил инерции. Анализ структуры волнового изгибающего момента для судна, симметричного относительно миделя, показал, что основную роль играют силы инерции при вертикальной качке. Хотя наибольшие ускорения, обусловленные вертикальной качкой, превышают таковые при вертикальной качке, но вызванные ими силы инерции в разных оконечностях имеют противоположные знаки. В результате изгибающий момент в миделевом сечении от сил инерции при килевой качке оказывается мал.

Рис. 34. Характерное положение корпуса движущегося корабля в штормовом море. Носовая часть корпуса активно взаимодействует со встречной волной, оставляя среднюю и кормовую части корпуса в относительно спокойном состоянии.
Было показано, что за счет сил инерции при вертикальной качке волновой изгибающий момент у судов с прогибом на тихой воде при прочих равных условиях заметно (примерно на 20 – 30 %) больше, чем у судов с перегибом. При статической постановке на волну волновой изгибающий момент зависит только от формы корпуса (и, естественно, от характеристик волны), но не зависит от распределения нагрузки по длине судна. Динамическая постановка на волну такую зависимость обнаруживает. К этому вопросу мы еще вернемся.
Развитие теории качки до настоящего времени далеко от завершения, это обусловлено тем, что структура волновой нагрузки очень сложна. Наличие поступательной скорости хода судна приводит к появлению многочисленных слагаемых, так или иначе влияющих на волновой изгибающий момент (хотя некоторые из них и не оказывают влияния на качку, будучи самоуравновешенными). В результате волновой момент может весьма существенно изменяться при различных скоростях хода судна, что также не обнаруживается при статической постановке на волну.
Тем не менее, статическая постановка на волну до сих пор не потеряла свою привлекательность по причинам исключительной простоты и наглядности. Отказавшись от этого метода по существу, современные исследователи часто используют его форму, приводя волновой момент, рассчитанный тем или иным методом, к высоте «эквивалентной» или «эффективной» волны, при статической постановке на которую изгибающий момент имеет ту же величину.
Установление зависимости между изгибающими моментами на тихой воде и волновым имело большое практическое значение. Анализ показал, что для сухогрузных судов в полном грузу характерен перегибающий момент на тихой воде, для танкеров – прогибающий. Следовательно, при прочих равных условиях волновой момент у танкера будет заметно больше, чем у сухогруза. Это нашло отражение в Нормах прочности: допускаемые напряжения для танкеров принимались меньшими, чем для сухогрузов. Такое положение могло показаться нелепым, ведь концентрация напряжений (которая прямо не учитывалась) в палубных перекрытиях танкеров меньше, чем у сухогрузов с большими палубными вырезами. Но действие сил инерции от вертикальной качки приводило к тому, что напряжения в корпусе танкера на одной и той же волне были больше, чем у аналогичного сухогруза.
Оптимизации распределения масс вдоль корпуса корабля
Влияние распределения масс по длине судна на величину волнового изгибающего момента объясняется достаточно просто. Рассмотрим положение судна на подошве волны (см. рис.35). В этом положении, как показывают расчеты линейной качки на регулярном волнении, центр тяжести (ЦТ) судна несколько погружается. Силы инерции от вертикальной качки, действующие на носовую и кормовую половины судна, направлены вниз (против ускорения, знак которого противоположен знаку перемещения). Эти силы уравновешиваются дополнительными силами поддержания (обратим внимание на то, что здесь не учитывается искривление волновой ватерлинии – оно определяет главную часть возмущающих сил и уже учтенный момент при статической постановке на волну). При разнесении масс к оконечностям (перегибе на тихой воде) равнодействующие сил инерции для половинок судна будут приложены дальше от миделя, чем равнодействующие сил поддержания, а при концентрации вблизи миделя (прогибе) – наоборот.

Рис. 35. Схема действия сил при вертикальной качке на подошве волны. а – судно с перегибом на тихой воде; б – судно с прогибом на тихой воде. И – силы инерции; П – дополнительные силы поддержания. Разность плеч сил для наглядности преувеличена.
В результате при перегибе дополнительный изгибающий момент от сил инерции действует против основного, обусловленного кривизной поверхности воды в волне, а при прогибе – в ту же сторону.
Авторами данной работы было обнаружено, что при определенном несимметричном относительно миделя распределении нагрузки можно существенно уменьшить волновой изгибающий момент за счет использования сил инерции при килевой качке. Напомним, у симметричного судна эти силы слабо влияют на волновой момент. Схема такого распределения и дополнительные силы инерции, возникающие при этом, показаны на рис.36.
Поскольку качка всегда отстает от возмущающей силы, на подошве волны судно имеет дифферент на нос, как показано на рисунке 36 б.

Рис. 36. Схема действия сил при килевой качке на подошве волны. а) – схема изменения нагрузки: 1 – нагрузка уменьшается; 2 – нагрузка увеличивается; б) – изменение сил инерции.
Предлагаемое изменение распределения нагрузки можно представить как встречный перенос двух пар грузов, причем большие по величине грузы переносятся на меньшее расстояние (рис. 36,а). В результате абсцисса ЦТ судна, величина радиуса инерции масс, которая определяет кинематические параметры килевой качки, изгибающий момент в миделевом сечении остаются постоянными. Но при килевой качке такое перераспределение нагрузки создает самоуравновешенную систему сил, показанную на рис.36,б изгибающий момент от которой по знаку всегда противоположен волновому. Как показали многовариантные расчеты, сравнительно небольшое (3–5% от водоизмещения) перераспределение масс на судне может снизить волновой изгибающий момент примерно на 10%. Архитектурно-конструктивный тип судна, реализующий предлагаемое решение, защищен патентом РФ № 2137660.
В середине ХХ века стала развиваться нелинейная теория бортовой качки. Традиционная линейная теория дает удовлетворительные результаты при малых амплитудах качки, не представляющих особой опасности для судна. При бортовой качке большой амплитуды, способной привести к опрокидыванию, сильно проявляется нелинейность восстанавливающего момента (непрямолинейность диаграммы плеч статической остойчивости) и сопротивления наклонениям, зависимость которого от скорости приближается к квадратичной. Нелинейность килевой качки при больших амплитудах долгое время не привлекала внимания исследователей. Видимо, одним из препятствий являлась сложность уравнений качки. По мере развития вычислительной техники расширялись возможности исследования сложных процессов, в том числе нелинейной продольной качки. Одно из направлений решения этой задачи – линеаризация, когда нелинейные эффекты сравнительно слабы. Более универсальным является численное решение уравнений шаговым методом, когда задается некоторый шаг по времени и при некоторых (в частном случае нулевых или полученных линейным расчетом) начальных условиях последовательно вычисляются параметры качки и обусловленные ею волновые нагрузки на каждом шаге.
Нелинейность продольной качки становится существенной, когда в какие-то моменты времени палуба заливается волнами, либо днище выходит из воды. В отличие от уравнения бортовой качки, в уравнениях продольной качки появляется множество дополнительных слагаемых, связанных не только с изменением характеристик ватерлинии, но и с формой шпангоутов. Вход шпангоута в воду при наличии плоского днища сопровождается практически мгновенным появлением значительных сил инерции (и сопротивления) воды, которые носят ударный характер. Менее резкие удары обнаруживаются и при быстром увеличении ширины шпангоутов в надводной части в носовой или кормовой оконечности – удары в развал борта. Линейная теория качки не позволяла рассчитывать возникающие при этом нагрузки. Поэтому задача решалась в два этапа: обычным линейным расчетом определялись кинематические параметры качки (естественно, без учета ударов, изменяющих эти параметры), а затем, в зависимости от скорости соударения и формы шпангоута в районе удара, рассчитывались возникающие нагрузки. Определению ударных нагрузок при слеминге посвящено значительное количество работ, рассмотрение которых выходит за рамки данной книги.
Остановимся здесь на одном аспекте этой проблемы. Не вдаваясь в подробности, укажем, что величина ударной нагрузки зависит от производной присоединенной массы по глубине погружения шпангоутного контура (его осадке) dm /dz.. Исследованиями волновых нагрузок занимались специалисты разного профиля – в области судовой гидродинамики и прочности, естественно, со своей точки зрения. «Прочнисты» установили, что среди множества слагаемых волновой нагрузки определяющее влияние на силу удара оказывает именно слагаемое, содержащее dm /dz.. Используя формальный математический подход, они получили в этом слагаемом коэффициент, равный 1. Приблизительно в то же время или несколько позже (примерно в конце 60-х - начале 70-х гг. ХХ века) методами гидродинамической теории продольной качки в этом же слагаемом был получен коэффициент 0,5. Таким образом, выяснилось, что два указанных подхода при одних и тех же параметрах качки судна дают значения ударных нагрузок, различающиеся в два раза. Одному из авторов книги довелось присутствовать на конференции, где докладчик, приводя результаты своих исследований по проблеме слеминга, говорил приблизительно следующее: «Вот такие получаются результаты при двух значениях этого коэффициента. Пусть специалисты разберутся в этом вопросе». Прошло немного лет, и было окончательно установлено, что правильным было значение 0,5.
Нагрузки на корпус при качке корабля
Как показали исследования нелинейной продольной качки на регулярном волнении, выполненные авторами, при значительной интенсивности волнения нелинейность вертикальной качки проявляется более значительно, чем килевой. Перемещения от вертикальной качки при погружении (для плавбазы «Содружество») получились примерно на 20 % меньше, чем при всплытии. Физически это обстоятельство вполне объяснимо: при погружении площадь ватерлинии заметно увеличивается, вместе с ней увеличиваются и восстанавливающие силы, что приводит к уменьшению перемещения. При килевой качке полнота ватерлинии меняется намного слабее, поэтому разница между положительными и отрицательными амплитудами составила примерно 1 %. Размахи обоих видов качки (суммы абсолютных значений амплитуд), как отмечается в различных источниках, мало отличаются от полученных линейным расчетом.
Более неожиданными явились результаты нелинейных расчетов волновых изгибающих моментов. При достаточно малых амплитудах волн средний волновой момент (с учетом знака амплитуды, т.е. как бы фиктивный момент на тихой воде) принимал положительные значения (перегиб), но по мере увеличения амплитуды он становился отрицательным (прогиб), достигая большой величины. В результате с ростом амплитуды волны в реально возможном диапазоне перегибающий волновой момент, достигнув максимума, начинал уменьшаться, а прогибающий быстро нарастал. Физически разница между перегибающим (на вершине волны) и прогибающим (на подошве волны) моментами вполне объясняется той же причиной, что и для вертикальной качки, т.е. изменением полноты действующей ватерлинии. Однако это объяснение относится к качественной картине явления, но не к количественной, поскольку с ростом амплитуды волны силы гидростатической природы, вызывающие изгиб корпуса, всегда растут, независимо от изменения полноты ватерлинии. Очевидно, что общий изгиб судна на волнении в значительной степени определяется силами гидродинамической природы.
Современные расчеты поведения судов на нерегулярном волнении, как правило, базируются на линейных моделях. Для заданного (стационарного) режима волнения обычно используется спектральная теория. В этом случае ординаты процесса морского волнения представляются в виде бесконечного тригонометрического ряда по частотам Ωk
([Екимов,1966],с.89):
 (52)
(52)
где: Uk и Vk - некоррелированные случайные величины со средними, равными нулю, и с одинаковыми дисперсиями DUk = DVk
=Dk. Плотность дисперсий, т.е. производная Sx(Ω) = dDk / dΩ, называется спектральной плотностью (спектром) процесса, а дисперсия всего процесса равна сумме дисперсий всех элементарных гармоник. Напомним, что дисперсия (при нулевом математическом ожидании) характеризует интенсивность случайного процесса и имеет размерность квадрата соответствующей величины. Так, для процесса морского волнения связь между высотой волны с 3%-ной обеспеченностью
h3%, которая служит мерой интенсивности волнения в нашей стране, и дисперсией волновых ординат Dв выражается формулой ([Екимов,1966], c.152)
Dв= 0.143 ( h3%/2)2 (53)
Часто бывает удобнее иметь дело с величиной  , размерность которой совпадает с размерностью соответствующей величины и которую обычно называют среднеквадратическим отклонением, а в судостроительной литературе – стандартом этой величины (иначе – стандартным отклонением). Стандарт – это некоторое осредненное положительное значение случайной величины.
, размерность которой совпадает с размерностью соответствующей величины и которую обычно называют среднеквадратическим отклонением, а в судостроительной литературе – стандартом этой величины (иначе – стандартным отклонением). Стандарт – это некоторое осредненное положительное значение случайной величины.
Заметим, что спектр морского волнения можно рассчитать по известным формулам (их предложено несколько) в зависимости от высоты h3% и среднего периода волн Тср; при необходимости последний можно определить по приближенной формуле, например, 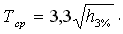
Судно рассматривается как линейная динамическая система, свойства которой описываются линейными дифференциальными уравнениями. Морское волнение для судна рассматривается как входной процесс, а в качестве выходного процесса (реакции системы на внешнее воздействие) могут рассматриваться параметры качки, волновые изгибающие моменты и другие характеристики. Обратим внимание на то, что реакция должна линейно зависеть от величины входного воздействия. Тогда, согласно формуле А.Я. Хинчина, спектр выходного процесса ([Екимов,1966], с. 114)
Sy(ω) = ay²(ω)Sx(ω) . (54)
Интегрируя спектр выходного процесса, можно получить его дисперсию. Если процесс нормальный (ординаты распределяются по нормальному закону, что считается справедливым для процесса морского волнения), а спектр узкий (на определении этого понятия мы не останавливаемся, но укажем, что морское волнение часто обладает широким спектром, но спектр вызванных им процессов обычно узкий), то амплитуды процесса распределяются по закону Рэлея, а амплитуду y(Q) с заданной обеспеченностью (вероятностью превышения) Q можно вычислить по формуле 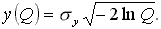
Можно решить и обратную задачу – задаваясь обеспеченностью, вычислить соответствующую ей амплитуду.
В первые годы применения вероятностных методов для оценки воздействия нерегулярного волнения на суда, в частности, общей продольной прочности судовых корпусов, следуя В.В. Екимову и А.А Курдюмову, использовался именно такой подход, причем выбирался наихудший (наиболее опасный) режим волнения. Почти всегда это было волнение наибольшей балльности, задача состояла лишь в выборе среднего периода волнения, который при одной и той же интенсивности волн может изменяться в достаточно широких пределах. Кроме того, следовало решить проблему выбора обеспеченности экстремального волнового воздействия (изгибающего момента). Но опыт использования такого подхода выявил один серьезный недостаток, который заключался в следующем. Большие суда сильно реагируют только на наиболее интенсивное волнение, которое встречается редко. На малые суда сравнительно слабое и часто повторяющееся волнение воздействует достаточно заметно. Поэтому вероятностный расчет на наиболее опасный режим волнения ставит большие суда в невыгодное положение. Практически это значит, что корпуса больших судов, спроектированные на основе расчета прочности при наиболее опасном режиме волнения, будут иметь избыточную прочность и, следовательно, массу.
В настоящее время принято использовать другой подход, известный как полновероятностная схема расчета. В простейшем виде основную формулу расчета волновых воздействий по этой схеме можно записать так: Q(ym) = ∑ p( h3%) Q (ym|h3%).
Здесь ym – некоторая заданная (опасная) амплитуда выходного процесса, Q - ее обеспеченность; p(h3%) - вероятность того или иного режима волнения (в сумме все эти вероятности равны 1) Q (ym |h3%) - так называемая условная вероятность, т.е. в данном случае обеспеченность величины ym в соответствующем режиме волнения. Для малых судов условные вероятности на умеренном волнении достаточно велики, для больших – малы, так что полновероятностная схема расчета обеспечивает более правильный учет условий эксплуатации различных судов.
Рассмотренный подход нашел широкое применение при решении задач прочности судов. Если рассматривается предельная прочность (наибольшая нагрузка один раз за весь срок службы судна), обеспеченность принимается равной 10-8, если усталостная прочность – например, 10-5. Известно, что методы теории вероятностей применимы лишь к массовым и практически однородным явлениям. Поэтому среди специалистов возникали дискуссии относительно принципиальной возможности использования вероятностных методов для оценки крайне редких экстремальных воздействий. Имеющиеся экспериментальные данные, как отмечается в специальной литературе, в целом неплохо согласуются с вероятностными оценками экстремальных волновых изгибающих моментов. Однако наши расчеты продольной качки по полновероятностной схеме дают сильно завышенные оценки амплитуд с очень малыми обеспеченностями. Эти расхождения можно объяснить нелинейностью восстанавливающих сил и сил сопротивления качке.
Таким образом, можно считать, что в настоящее время перспективными являются два принципиально различных направления в исследовании внешних сил, возникающих при качке судов на волнении: 1) исследование нелинейной качки, преимущественно численными методами; 2) использование вероятностных методов. Несмотря на их различия, между ними имеются области соприкосновения. Например, поведение судов при прохождении волнового пакета девятый вал. Давно замечено, что при сильном нерегулярном волнении наблюдаются пакеты волн, имеющие приблизительно регулярную структуру. Реакцию судна (качку, общий продольный изгиб, ударные нагрузки) на такие пакеты волн целесообразно исследовать детерминистическими методами. В этом направлении ряд работ выполнен в г. Николаеве (Украина) под руководством В.П. Суслова. Другой вариант – численные нелинейные расчеты для нерегулярного волнения – получил меньшее распространение, хотя для современной компьютерной техники такие расчеты не представляют принципиальных трудностей.
Обратим внимание на то, что расчеты волновых нагрузок (применительно ко всем 6 возможным видам качки, включая дополнительные, существующие только на волнении) позволяют получить исходные данные не только для оценки общей продольной прочности (вертикального изгиба) и местной прочности при продольной качке. На косом курсе по отношению к волнению возникают горизонтальный изгиб и общее скручивание корпуса, напряжения от этих воздействий также могут быть значительными. В частности, у судов открытого типа с большими люковыми вырезами проблема прочности и жесткости при кручении стоит достаточно остро. Решение задач управляемости и ходкости на волнении также требует знания нагрузок, определяемых методами судовой гидродинамики.
Проблема определения нагрузок, действующих на суда, плавающие на произвольном волнении, очень сложна. Она требует решения большого количества вспомогательных задач, среди которых назовем следующие:
- Теоретическое установление структуры гидродинамических сил.
- Определение гидродинамических коэффициентов (присоединенных масс и сопротивления – демпфирования).
- Моделирование морского нерегулярного волнения.
- Аналитическое или численное описание поверхности судна.
- Вычисление усилий, действующих на элемент смоченной поверхности и на судно в целом. После решения этих задач могут рассчитываться реакции судна на волновые воздействия.
Указанные задачи решаются преимущественно специалистами в конкретной, сравнительно узкой области знаний. Мы здесь коснемся лишь одной, простой и понятной задачи – численного моделирования волнения с заданными характеристиками. Результаты – численные модели морских волн – далее используются для нелинейного расчета параметров качки и волновых нагрузок на судно. Напомним, что и качка, и изгиб корпуса судна в целом и его отдельных конструкций вызываются одними и теми же нагрузками; решение уравнений качки позволяет вычислить действующие нагрузки.
Моделирование морского волнения в расчетах прочности корпуса
В традиционных расчетах качки профиль волны считается синусоидальным, вид его уравнения зависит от условий конкретной задачи (от того, с направлением какой координатной оси совпадает вектор скорости бега волн или какова величина угла между ними). Например, при движении судна навстречу волнам уравнение волнового профиля можно записать в виде:
ζв = rв cos( kx + σt ) ,
где: k - частота формы волны (волновое число); σ - частота волны.
В теории волн конечной высоты профиль волны считается трохоидальным, соответствующее уравнение (51) или (51а) записано выше. И синусоидальный, и трохоидальный профиль симметричен относительно вертикали, проходящей через вершину или подошву волны. Наблюдения показывают, что профиль ветровой волны свойством симметрии не обладает: его подветренный склон круче, чем наветренный. Отдельные волны по форме приближаются к треугольным. Аналитическое описание любого периодического профиля возможно с помощью тригонометрических рядов (Фурье). Например, для несимметричной трохоиды можно использовать выражение

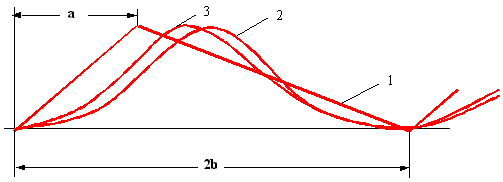
Рис. 37. Варианты нетрадиционных волновых профилей. 1 - треугольная волна, 2 – трохоида и 3 – несимметричная трохоида
Треугольный профиль при заданном параметре асимметрии с описывается такими зависимостями:

Здесь параметр с характеризует смещение вершины профиля, отнесенное к полудлине волны: c = (1-a/b)
Подобным же образом можно задавать, например, пакеты волн. Заметим, что профиль волны еще не определяет распределение давлений в ней. Для синусоидального волнения можно сравнительно просто ввести редукционные коэффициенты, которые учитывают орбитальное движение частиц жидкости в волне (вода на вершине волны легче, чем на подошве); при сложении гармоник с различными частотами задачу определения редукционных коэффициентов необходимо решать особо.
Для моделирования нерегулярного волнения можно использовать спектральное разложение в форме (52), но, как показал опыт, зависимость типа (52) лучше использовать несколько иначе. Задается несколько (например, 30) частот; они могут быть или равноотстоящими на числовой оси, или расположенными неравномерно. Каждой частоте соответствует вполне определенная (не случайная, как в выражении (52)) амплитуда, подсчитанная в соответствии с формулой спектральной плотности волновых ординат для требуемого режима, что гарантирует получение нужной, а не случайной интенсивности волнения (и нужного спектра). Фазовые углы принимаются случайными, при этом ограничиваются только одной из двух использованных в формуле (52) тригонометрической функцией – синусом или косинусом. Сложение всех полученных гармоник дает реализацию требуемой случайной функции любой длительности. Функция не будет периодической. Пример полученного таким образом профиля показан на рис.38.

Рис. 38. Запись профиля нерегулярной волны в одной точке.
Как известно, реальное волнение характеризуется не только нерегулярностью в смысле несовпадения элементов отдельных волн, но и трехмерностью, т.е. отклонениями направления распространения отдельных волн от генерального направления. Поведение судна на трехмерном волнении не такое, как на двухмерном, поскольку уже невозможно получить чисто поперечную (судно лагом к волне) или продольную (встречное или попутное волнение) качку. Считается, что энергия трехмерных волн распределена в пределах сектора ± 90° от генерального направления и пропорциональна cos4 φ или cos² φ, где φ - угол между направлением распространения элементарной волны и генеральным направлением. Для численных расчетов с использованием трехмерной модели волнения необходимо генерировать уже не профиль волны, а волновое поле, имитирующее взволнованную поверхность моря. Примеры моделирования такого волнения приведены в предыдущей главе.
1. Принятые обозначения формулируются в курсе Физики А.В. Астахова и Ю.М. Широкова [1980]

2. В соответствии с ранее принятыми обозначениями:
3. Подробному толкованию точек Ѓ‚ѓ , а также критического угла 2 Θ , посвящена следующая глава.
4. Цифры в кружочках, встречающиеся в тексте, означают позиции на рисунках
5. Здесь и далее замечание: z=z/T - означает, что величина z нормирована до единицы.
6. Решение всех перечисленных задач пока не поддерживается правилами Морского регистра России.
7. Цитируется по книге А.Н. Крылова «Мои воспоминания», Л.: Судостроение, 1979. С.352.
 История штормовой мореходности (от древности до наших дней)
История штормовой мореходности (от древности до наших дней)
§ 1. История кораблестроения как поиск непротиворечивого диалога с океаном
§ 2. Условия штормового мореходства и морская инфраструктура
§ 3. Проектные особенности корабля повышенной штормовой мореходности
§ 4. Проработка перспективных проектов кораблей повышенной мореходности
Морское дело и научно-техническое творчество юношества
Краткий толковый словарь морских и кораблестроительных терминов
Аннотированный список использованной литературы
Содержание


 (1)
(1)


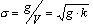
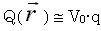








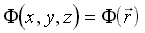 . Решение ищется в виде поля скалярного потенциала скорости:
. Решение ищется в виде поля скалярного потенциала скорости: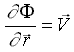 , удовлетворяющего уравнению Лапласа:
, удовлетворяющего уравнению Лапласа:

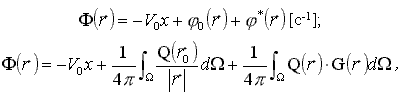 (2.0)
(2.0) 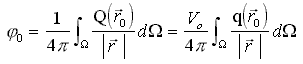 (2.2)
(2.2) (2.3)
(2.3)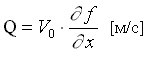 ( 3 )
( 3 )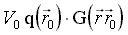 будет определять потенциал течения, обусловленного влиянием источников, распределенных по всей поверхности корпуса, на свободную поверхность пересекаемой им тяжелой жидкости.
будет определять потенциал течения, обусловленного влиянием источников, распределенных по всей поверхности корпуса, на свободную поверхность пересекаемой им тяжелой жидкости.
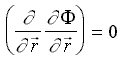 ( 4 )
( 4 ) ( 5 )
( 5 )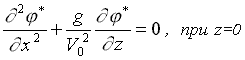 ( 6 )
( 6 )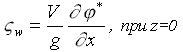 (7)
(7) (8)
(8) , а волнообразующий потенциал как:
, а волнообразующий потенциал как: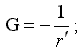 (9)
(9)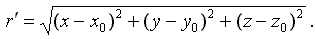 .
.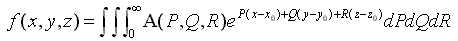 (10)
(10) , получим:
, получим: 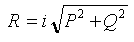 .
. (11)
(11)
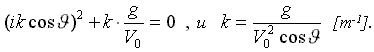 (13)
(13) .
. внутренний интеграл, по параметру φ обращается в нуль:
внутренний интеграл, по параметру φ обращается в нуль:
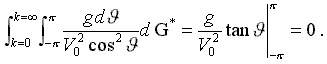 .
.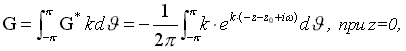 (14)
(14)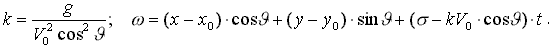
 (15)
(15)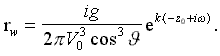 (16)
(16) (17)
(17)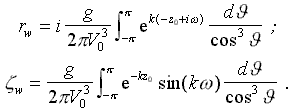
 (18)
(18)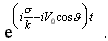

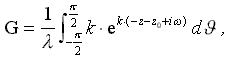 (14’)
(14’)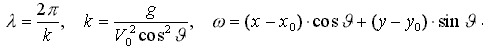
 (19)
(19)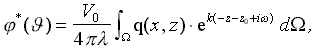 (20)
(20)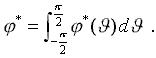


 (21.1)
(21.1) (21.2)
(21.2)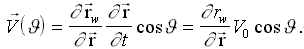
 (22.1)
(22.1)
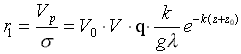 (22.2)
(22.2)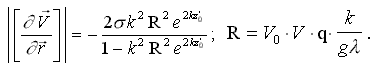
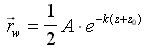 . В соответствии с трохоидальной теорией, локальная траектория частиц жидкости описывается дугой окружности с радиусом rw, зависящим от текущей аппликаты: z, для данной частицы жидкости zw и от амплитуды волны на поверхности:
. В соответствии с трохоидальной теорией, локальная траектория частиц жидкости описывается дугой окружности с радиусом rw, зависящим от текущей аппликаты: z, для данной частицы жидкости zw и от амплитуды волны на поверхности:
 . Скорость движения элементарных частиц определяется через произведение частоты колебаний и радиуса дуги траектории:
. Скорость движения элементарных частиц определяется через произведение частоты колебаний и радиуса дуги траектории: 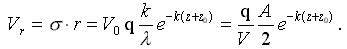

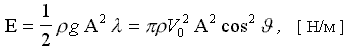 (23)
(23)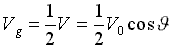 (для глубокой воды). Излучение корабельных волн ведется в диапазоне:
(для глубокой воды). Излучение корабельных волн ведется в диапазоне: 

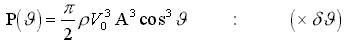 (24)
(24)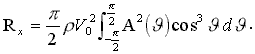 (25)
(25)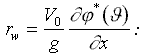 (7) Þ (20)
(7) Þ (20) (16) Þ (17)
(16) Þ (17)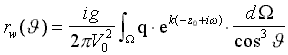 (26)
(26)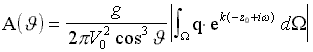 (27)
(27)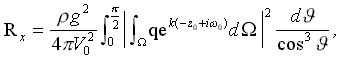 (28)
(28)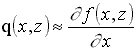 ; Ω0 = x0 cosφ по Мичеллу): Ω0 = x0 cosφ + y0 sinφ (по Кочину).
; Ω0 = x0 cosφ по Мичеллу): Ω0 = x0 cosφ + y0 sinφ (по Кочину).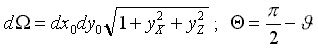 - угол фронта.
- угол фронта. 
 . Амплитуда волны на свободной поверхности жидкости (z=0), полученная в результате излучения с единичной площадки на обшивке корпуса, представляется как:
. Амплитуда волны на свободной поверхности жидкости (z=0), полученная в результате излучения с единичной площадки на обшивке корпуса, представляется как: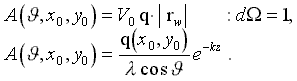 (29)
(29)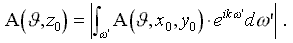 (31)
(31) (32)
(32)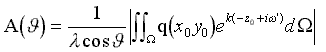 (33)
(33)
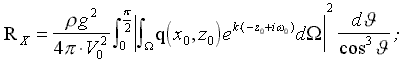 (28’)
(28’) (25’)
(25’) (33’)
(33’)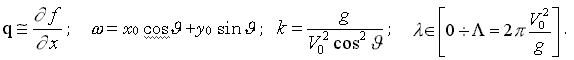
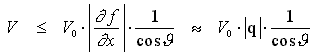 (35)
(35)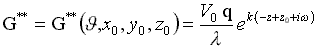 (36)
(36)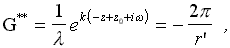 (37)
(37)
 (38)
(38)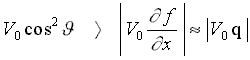
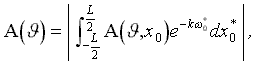 (39)
(39)
 (40)
(40)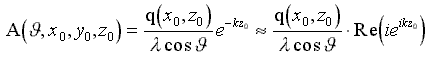 (41)
(41)
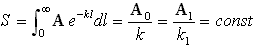 . Новая амплитуда волнового гребня и связанная с ним частота формы волны могут быть согласованы с условием отсутствия обрушения гребня стоячей волны:
. Новая амплитуда волнового гребня и связанная с ним частота формы волны могут быть согласованы с условием отсутствия обрушения гребня стоячей волны: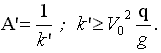 (45)
(45)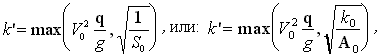 (46)
(46)
 может привести к нарушению стационарности картины волнообразования, что обычно наблюдается в опытовых экспериментах и объясняется свойствами потенциала (40)
может привести к нарушению стационарности картины волнообразования, что обычно наблюдается в опытовых экспериментах и объясняется свойствами потенциала (40) 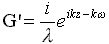 , допускающего осцилляционные решения также и в направлении аппликаты z.
, допускающего осцилляционные решения также и в направлении аппликаты z.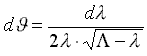 – выражение для дифференциала;
– выражение для дифференциала; 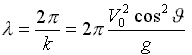 – фазовая длина волны; L=2pV02/g
– критическая или максимальная длина поперечной волны;
– фазовая длина волны; L=2pV02/g
– критическая или максимальная длина поперечной волны;  – аналог волнового число Маха; C=V0 /M – фазовая скорость волны;
H=A·l·M/4 – функция Кочина. Тогда основные расчетные формулы примут вид:
– аналог волнового число Маха; C=V0 /M – фазовая скорость волны;
H=A·l·M/4 – функция Кочина. Тогда основные расчетные формулы примут вид: 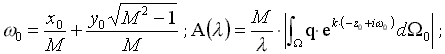
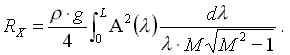
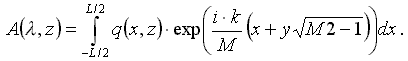 (47)
(47) где L - длина между перпендикулярами; Ni - количество шпангоутов; Np - допустимое количество точек аппроксимации, приходящихся на один период рассчитываемой корабельной волны.
где L - длина между перпендикулярами; Ni - количество шпангоутов; Np - допустимое количество точек аппроксимации, приходящихся на один период рассчитываемой корабельной волны.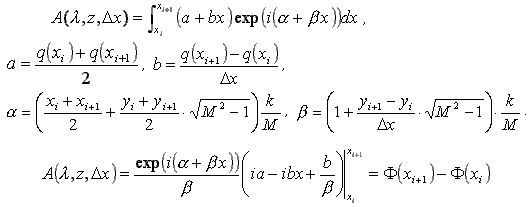
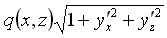 , достигаемому вблизи штевней. Если заранее рассчитать такие максимумы, то критерием достижения заданной точности при вычислении интеграла по ватерлиниям явится выражение e-kz| max(q·Ω)| > eps.
, достигаемому вблизи штевней. Если заранее рассчитать такие максимумы, то критерием достижения заданной точности при вычислении интеграла по ватерлиниям явится выражение e-kz| max(q·Ω)| > eps. (48)
(48)
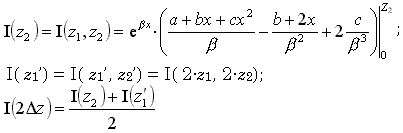

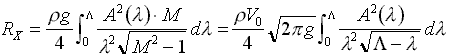 (49)
(49) 

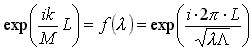 , где: L - длина судна. Если допустить “проход” трех периодов волн в полученной зависимости от аргумента λ, тогда
, где: L - длина судна. Если допустить “проход” трех периодов волн в полученной зависимости от аргумента λ, тогда
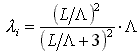 , а отношение λ / L = 2p·FN2.
, а отношение λ / L = 2p·FN2. был использован рекурсивный алгоритм, основанный на использовании полиномов Гаусса 4-й степени, которые удовлетворительно аппроксимируют функции с особенностями на границах интервала интегрирования. При вычислении интеграла
был использован рекурсивный алгоритм, основанный на использовании полиномов Гаусса 4-й степени, которые удовлетворительно аппроксимируют функции с особенностями на границах интервала интегрирования. При вычислении интеграла 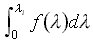 использовался традиционный «метод трапеций», так как его аппроксимации не приводят к разрывам решений с осциллирующими функциями.
использовался традиционный «метод трапеций», так как его аппроксимации не приводят к разрывам решений с осциллирующими функциями.
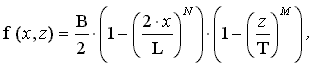


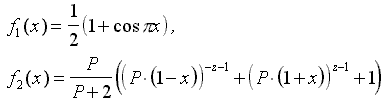


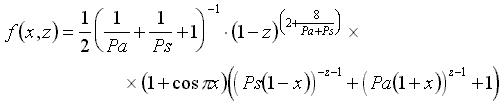



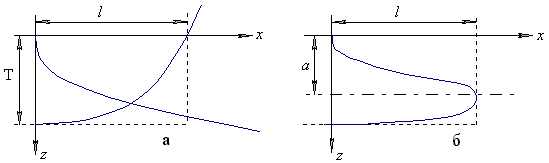

 , где: l - относительная длина кормового подзора.
, где: l - относительная длина кормового подзора.








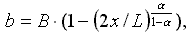 где: L и В – соответственно длина и ширина судна; α - коэффициент полноты ватерлинии.
где: L и В – соответственно длина и ширина судна; α - коэффициент полноты ватерлинии. (51)
(51)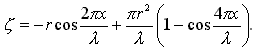 (51a)
(51a)


 (52)
(52) , размерность которой совпадает с размерностью соответствующей величины и которую обычно называют среднеквадратическим отклонением, а в судостроительной литературе – стандартом этой величины (иначе – стандартным отклонением). Стандарт – это некоторое осредненное положительное значение случайной величины.
, размерность которой совпадает с размерностью соответствующей величины и которую обычно называют среднеквадратическим отклонением, а в судостроительной литературе – стандартом этой величины (иначе – стандартным отклонением). Стандарт – это некоторое осредненное положительное значение случайной величины.