 (1)
(1)ДЖОН ГЕНРИ МИЧЕЛЛ И ЕГО НАУЧНОЕ НАСЛЕДИЕ
А.Ш. Готман
Как мне уверить в доблестях твоих
Тех, до кого дойдут мои страницы?
Шекспир
Имя Мичелла известно всем, кто занимается гидромеханикой и теорией корабля, а также теорией упругости, но о нём самом нам известно очень мало. Из ссылок под его публикациями известно только, что он жил в Австралии и работал в Мельбурнском университете.
Для того чтобы был ясен масштаб личности Мичелла и его место в науке, интересно проследить историю решения задачи о волновом сопротивлении судов.
Ещё в древности люди понимали, что существует сопротивление воды движению судна, а потому придавали корпусу обтекаемую форму. Самый первый научный труд, посвящённый движению тел в воде и в воздухе, был написан Леонардо да Винчи (1458-1519). Эта его работа была опубликована только через 300 лет и называлась «О движении и измерении воды».
1687 год – Исаак Ньютон (Англия) впервые попытался создать теорию сопротивления воды движению тел в жидкой среде в труде «Математические начала натуральной философии». Гипотеза Ньютона состояла в том, что плотность жидкости оказывает сопротивление движению за счёт ударов жидких частиц о переднюю часть тела. Его формула квадратичного закона зависимости сопротивления от скорости явилась большим научным открытием.
1746 год – П. Буге в Париже написал «Трактат о корабле, о его конструкции и его движении».
1749 год – Леонард Эйлер (Россия) написал монографию «Корабельная наука», а в 1778 году – «Полное умозрение строения и вождения кораблей». Эйлер взамен теории ударов Ньютона разработал теорию обтекания и получил формулу зависимости сопротивления воды от площади миделя, удлинения корпуса судна, плотности жидкости и квадрата скорости его движения.
1756 год – Бэрд в Англии провёл первые испытания моделей судов в опытовом бассейне длиной 10 метров.
1775 год – Ж.Л. Д’Аламбер, Э. Боссю, М.Ж.А. Кондорсе (Франция) провели первые систематические испытания моделей судов в бассейне гравитационного типа.
1847 год – Джордж Габриель Стокс впервые решил задачу об установившихся волнах конечной амплитуды на поверхности глубокой жидкости.
1871 год – Вильям Фруд (Торквей, Англия) построил первый бассейн с тележкой, а в 1873 году разработал метод пересчёта сопротивления с модели на натуру, пользуясь законом гравитационного подобия, идея которого принадлежит Реху (1844).
1880 год – Д.И. Менделеев опубликовал работу «О сопротивлении жидкостей и о воздухоплавании». Он изложил основы современного учения о сопротивлении трения и указал на необходимость взаимосвязи теории и опыта при решении проблемы сопротивления воды движению судов. По его инициативе и поддержке в Петербурге был построен первый в России опытовый бассейн, носящий его имя.
1887 год – Лорд Кельвин – Томсон (Англия) решил задачу о корабельных волнах от движущегося импульса давления, используя теорию бесконечно малых волн.
1893 год – Джон Генри Мичелл решил задачу о волнах конечной амплитуды, в которой подтвердил известный результат Стокса о том, что угол при вершине волны не может быть меньше 120°, а также получил профиль волны и доказал, что наибольшее отношение высоты волны к его длине равно 0,142 [8a].
В библиографическом справочнике А.Н. Боголюбова «Математики механики» (1983) Дж. Мичеллу посвящена статья, в которой отмечены его работы в области математики, физики, гидравлики и теории упругости, а также указано, что он занимался теорией гироскопов, в теории упругости установил дифференциальные зависимости между составляющими напряжений (1899), дал решение двумерной задачи теории упругости (1899), исследовал напряжения, вызываемые в круглом диске сосредоточенными нагрузками. Отмечено, что его исследования о волновом сопротивлении корабля (1898) конструкторы начали использовать только через 30 лет. Из этой статьи видно, как отрывочны и неполны наши сведения о Мичелле.
Будучи в Мельбурне, я воспользовалась этим обстоятельством, чтобы собрать материалы о Мичелле. Мне было интересно познакомиться с историей Веслей колледжа, в котором учился Мичелл, поработать в библиотеках Мельбурнского университета, в котором он работал, полистать книги, некогда ему принадлежавшие, побеседовать с профессором Р. Лавом, который в 1932 году слушал лекции Мичелла по аэродинамике, и возложить цветы на его надгробье. Сведения об учителях Мичелла, об обстановке в Мельбурнском университете в годы его учёбы и работы, об отношении коллег к работам Мичелла, а также сведения о его жизни показались мне очень интересными. Единственное свидетельство о его жизни было опубликовано после смерти. Это был некролог, написанный братом Мичелла и профессором Т.Черри, который занял кафедру математики после ухода Мичелла на пенсию и хорошо его знал. Этот некролог был опубликован в заметках Лондонского Королевского общества [1], а затем перепечатан в работе Дж. Радека и Ф. Ниденфюра [2] в качестве предисловия к сборнику работ Джона Мичелла и его известного брата Антони Георга Малдона Мичелла. В этом некрологе сделан обзор научного наследия Мичелла. Здесь уместно отметить, как сказал Р. Лав в нашей беседе, что известен только один случай в истории науки, когда два брата получили звание почётных членов Королевского общества. Профессор Р. Лав сказал также, что брат Мичелла, инженер – кораблестроитель, был более известен при жизни, чем Джон Генри, благодаря разработкам, связанным с движителями. Он разработал упорный подшипник, который вскоре стал известен в Германии и использовался в судостроении.
В 1998 году научная общественность широко отмечала столетие статьи Мичелла о волновом сопротивлении судна. По инициативе профессора Эрнеста Така специальная сессия была посвящена Мичеллу и его статье о волновом сопротивлении на Международной конференции (EMAC '98) в Аделаиде в июле 1998 года. Несмотря на то, что прошло 100 лет со времени выхода статьи Мичелла о волновом сопротивлении и несмотря на появление большого количества работ крупных специалистов по гидромеханике и математике по волнам и волновому сопротивлению, его работа не устарела и не потеряла своего практического значения, потому что только интеграл Мичелла связывает величину волнового сопротивления с уравнением обводов корпуса судна. Однако в проблеме определения волнового сопротивления судов есть своя загадка. На всех расчётных кривых, полученных по линейным и нелинейным теориям, на коммерческих скоростях есть горбы и впадины, отсутствующие на экспериментальных кривых у всех типов водоизмещающих судов. Объяснения этому явлению нет. Та гипотеза, которая удовлетворяла исследователей в течение многих лет, была опровергнута экспериментом, проведённым автором [12]. И то, что за 100 лет это явление не получило объяснения, заставляет снова и снова возвращаться к работе Мичелла, как строго линейному решению.
Есть загадка и в жизни самого Мичелла. Почему такой талантливый учёный, решавший сложнейшие задачи ходкости и теории упругости, в 39 лет прекратил публикации своих научных работ и переключился на педагогическую работу и консультации для инженеров? Эта проблема особенно интересует австралийских учёных, потому что Мичелл является гордостью и легендой этой страны (хотя в Мельбурнском университете, где Мичелл учился и всю жизнь работал, нет даже мемориальной доски, а его обширная библиотека раскидана по разным отделам). Коллега Мичелла профессор Т. Черри в своё время писал: «Мичелл имел репутацию одного из ведущих учёных в мире, благодаря его исследованиям по гидродинамике и теории упругости, опубликованным в период с 1890 по 1902 год. В гидродинамике его статьи по свободным линиям тока и волновому сопротивлению судов являются работами большого значения, концепции которых и исполнение показали воображение и мастерство наивысшего порядка. Большинство его публикаций, однако, были по теории упругости, куда его вклад был наибольшим в период систематизации и обобщения в 19 столетии. Он был первым, кто сформулировал фундаментальные уравнения упругости в напряжениях, выполнил расчёт тонких пластин без сомнительных допущений, систематизировал и применил теорию изгиба и кручения балок и дал остроумные решения различных специальных задач. Эти исследования стали известны во время выборов его почётным членом Королевского общества» [10].
Джон Мичелл внёс достаточно большой вклад в науку, чтобы вызвать интерес не только к своим работам, но и к своей личности. Автор надеется, что тем, кому известно имя Мичелла, будет интересно познакомиться с его биографией и условиями жизни и работы.
Список всех опубликованных работ Мичелла приводится в Приложении I. Здесь рассмотрены только фундаментальные его работы. К ним относятся решение задачи о свободных линиях тока, задача о волнах конечной высоты и решение задачи о волновом сопротивлении судна. По теории упругости Мичеллем получен целый ряд решений, главным из которых является прямой метод определения напряжений. Им разработана точная теории изгиба пластин, а также получены новые методы для решения уравнений упругости. Мичеллу принадлежат решения следующих задач: расчёт напряжений в полубесконечных пластинах, вызванных сосредоточенной силой или распределением сил; расчёт напряжений в диске при действии сосредоточенной силы или касательных напряжений; расчёт напряжений в многосвязных пластинах, в пластинах с криволинейными границами и в кольцах; расчёт кручения вала переменного диаметра; изгиб консолей под действием разных нагрузок; разработан метод определения напряжений в телах вращения.
Интеграл Мичелла и загадка задачи о волновом сопротивлении
Теория поверхностных волн и сопротивления воды движению тел является одним из сложнейших разделов гидромеханики и теории корабля. Основы теории поверхностных волн были заложены О. Коши (1789 – 1857). Он сумел сформулировать граничные условия на свободной поверхности и привести их к простейшему виду. Путём исключения из кинематического и динамического условий неизвестного уравнения свободной поверхности, он получил для прогрессивных волн граничное условие на свободной поверхности в виде (ось z направлена вверх)
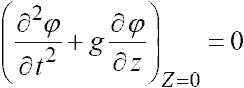 (1)
(1)
где j -потенциал скорости, g – ускорение силы тяжести, z = 0 -уравнение невозмущённой свободной поверхности, на которую Коши перенёс это условие с неизвестной взволнованной поверхности. Это условие позволило ему разработать теорию бесконечно малых волн на поверхности жидкости.
Теорию корабельных волн в конце 80-х годов прошлого века разработал Лорд Кельвин. Он преобразовал полученное Коши условие к виду
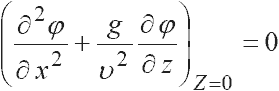 (2)
(2)
где вместо дифференцирования по времени t для установившегося движения жидкости дифференцирование выполняется по координате х.
Джордж Буддел Эри (1801 – 1892) получил основную зависимость между квадратом скорости и длиной l прогрессивной волны в виде
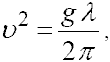 (3)
(3)
Зная приведенные выше решения, Мичелл приступил к задаче о волновом сопротивлении судов. Он начал свою статью [10a] словами: “...цель этой статьи состоит в том, чтобы дать общее решение задачи о волнах, продуцируемых судном данной формы, движущемся с постоянной скоростью в невязкой жидкости, и определить связанное с ними сопротивление движению судна. Единственное допущение, сделанное о форме судна, заключается в том, что касательная плоскость к поверхности корпуса составляет малый угол с диаметральной плоскостью. Это условие не удовлетворяется возле днища на миделе у современных судов, но эта часть корпуса не оказывает такого большого действия на волны и сопротивление, как нос и корма, где касательные составляют малый угол с направлением движения”. Формулируя это допущение, Мичелл исходил из того, что две системы корабельных волн движущегося судна отходят от носа и от кормы. Поражает то обстоятельство, что, не будучи инженером-кораблестроителем, он правильно учёл картину потока вокруг движущегося судна. Допущение о малом отношении ширины к длине судна позволило Мичеллу линеаризовать условие непротекания на поверхности корпуса, а затем по методу О. Коши перенести это условие на диаметральную плоскость и получить
 (4)
(4)
где: y=h (x,z) - уравнение поверхности корпуса судна.
С помощью граничных условий (2) и (4) Мичелл сформулировал краевую задачу. Эту задачу принято называть задачей Мичелла -Кельвина. Итак, жидкость считается идеальной и несжимаемой. Интегрируется уравнение Лапласа
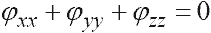 (5)
(5)
с граничными условиями на свободной поверхности (ось z направлена вниз)
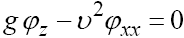 (6)
(6)
и условиями на корпусе судна
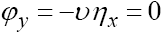 (7)
(7)
при у = 0, а также условием непротекания на дне jx= 0 при z = h (h –глубина жидкости).
Мичелл решил эту задачу методом Фурье и получил решение в виде интеграла, который носит название интеграла Мичелла. Этот трёхкратный интеграл записывается в виде
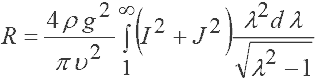 (8)
(8)
где
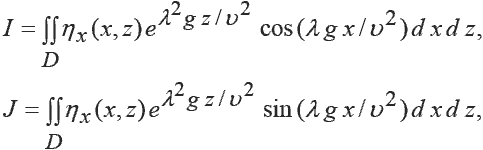 (9)
(9)
где D – область интегрирования, ограниченная диаметральным батоксом и плоскостью действующей ватерлинии. В конце рассмотренной выше работы Мичелл привёл формулу для расчёта волнового сопротивления судна, движущегося на мелководье, на 5 лет опередив работу Н.Е. Жуковского. Он даже привёл расчёт. Этот расчёт перепроверил проф. Э. Так (университет в Аделаиде). Он показал, что там, где Мичелл получил величину 0,620, на компьютере была получена величина 0,6157 [11].
Эта работа Мичелла оставалась незамеченной в течение почти 30 лет. Брат Мичелла писал: «Статья [10a], посвящённая волновому сопротивлению судна, потребовала огромной вычислительной работы не только при разработке, проверке и перепроверке теории и выводов, но также и в детальном арифметическом сравнении результатов теории с имеющимися записями экспериментальных данных для полномерных судов и их моделей. Только небольшая часть этой работы была опубликована. Тот факт, что статья появилась без детальных арифметических результатов или графических иллюстраций, отчасти был причиной того, что статья не была замечена теми, кто занимался проектированием судов, до тех пор, пока тридцать лет спустя, Виглей в Англии и другие в Германии не начали понимать её фундаментальное значение. Джон Мичелл никогда не старался привлечь внимание к своим работам, но отсутствие какого-либо отклика на такие работы, как "The wave resistance of a ship", неизбежно расхолаживало к продолжению остальных публикаций, содержащих фундаментальные исследования и требующих так много утомительного труда».
Принято оправдывать невнимание исследователей к статье Мичелла тем, что в ней не были приведены результаты расчётов. Можно поражаться тому, что, как рассказал мне Р. Лав, не имея даже арифмометра, вручную Мичелл выполнял такое сложное интегрирование. Это, конечно, был титанический труд.
Об этой работе Мичелла его коллега Т.Черри писал: «"The wave resistance of ship" [10а], с нашей точки зрения, наиболее значительная работа Мичелла по смелости концепции и математическому мастерству. Только через тридцать лет после опубликования этой работы Мичелла его формула была проверена экспериментально Виглеем (W.C.S. Wigley, Trans. Inst. Naval Architects, 1926-1927). Это было трудное дело, хотя бы только потому, что при измерении волнового сопротивления необходимо вводить коррективы для учёта влияния вязкости. Согласование достигнуто до 5% на высоких скоростях, где волновое сопротивление преобладает над силами вязкости».
В процитированном начале статьи [10a] Мичелл написал, что он хочет «дать» формулу для расчёта волнового сопротивления. Он рассчитывал, что инженеры поспешат воспользоваться его формулой, но он, по-видимому, не учёл, что в то время инженерам было не под силу выполнять такие громоздкие расчёты вручную. В двадцатые годы Виглей разработал серию из 15 моделей, отвечающих допущению Мичелла. Модели имели равное 10 отношение длины к ширине, аналитические обводы и постоянную осадку, что существенно облегчало расчёты по формуле Мичелла. Сравнение расчётов с результатами экспериментов Виглея показало, что формула Мичелла даёт качественный результат. С этого момента наступил новый период в истории задачи о волновом сопротивлении.
1926 год – Уилфред Виглей (Wilfred Cyril Sprye Wigley) опубликовал результаты испытаний серии из 15 моделей для проверки теории Мичелла.
1930 год – Георг Вейнблюм (Georg Weinblum) провёл испытания серии из 15 моделей с аналитическими обводами, уравнения которых отличались от уравнений моделей Виглея, но также отвечали допущениям Мичелла.
1957 год -Т. Инуи (T. Inui) выполнил экспериментальную проверку допущения Мичелла о возможности линеаризации граничных условий на корпусе судна. Он испытал большую серию моделей, спроектированных по линиям тока для разного распределения особенностей. При выборе оптимального распределения особенностей была использована теория Мичелла. Результаты эксперимента не совпали с расчётами.
1962 год – Х. Маруо (H. Maruo) получил теоретическое решение принципиально отличной от решения Мичелла задачи о судне с малой относительной осадкой, а не шириной.
До начала шестидесятых годов в области волнового сопротивления судов было выполнено не очень много работ, среди которых следует отметить работы Т. Хавелока (T. Havelock). Ситуация принципиально изменилась после Международного семинара по волновому сопротивлению, организованного по инициативе Георга Вейнблюма (Georg Weinblum) и Ричарда Коха (Richard Couch) в 1963 году в Анн Арборе. На этом семинаре была намечена большая программа работ, которую выполняли совместно теоретики и экспериментаторы всех судостроительных стран. В попытке улучшить теорию Мичелла учёные начали разрабатывать нелинейные теории волнового сопротивления.
1969 год -Е. Баба экспериментально доказал, что первые две носовые волны имеют ударный характер. Это открытие положило начало разработке теории ударных носовых корабельных волн.
1970 год – Ф.Огилви (T.F. Ogilvie) выполнил фундаментальную работу по использованию асимптотических методов в гидродинамике судна, в которой получил оценки различных членов разложения уравнений движения и граничных условий на свободной поверхности.
1975 год – Е. Баба (E. Baba) и К. Такекума (K. Takekuma), используя оценки Ф.Огилви, разработали теорию малой скорости, пытаясь избавиться, наконец, от горбов и впадин на расчётных кривых волнового сопротивления. Проверка этой теории показала, что она даёт хорошие результаты, когда числа Фруда меньше 0,2 и на высоких числах Фруда (где линейная теория Мичелла даёт хороший результат), а на коммерческих скоростях её результаты не совпадают с экспериментом.
1976 год – состоялся Международный семинар по теории волнового сопротивления, на котором обсуждались результаты исследований, выполненных за 13 лет, прошедших после семинара в Анн Арборе. Получить новую расчётную формулу для волнового сопротивления судов любой формы так и не удалось. Возникло много новых проблем.
После семинара в Токио усилия исследователей были направлены на разработку численных методов определения волнового сопротивления.
Говоря о точности вычислений по формуле Мичелла на компьютере, следует отметить очень важное обстоятельство, связанное с расчётами волнового сопротивления вообще. Как видно из формул (9), в подынтегральное выражение входит производная от уравнения поверхности корпуса, такимобразом, интегралы Мичелла представляют собой интегралы Стилтьеса, поэтому при численном интегрировании недопустимы сломы и скачки на поверхности интегрирования, которые неизбежны при использовании метода трапеций или Симпсона. С начала восьмидесятых годов в Чалмерском университете в Швеции начали разработку метода криволинейных панелей, чтобы сохранить гладкость поверхности интегрирования. В течение многих лет исследователи, выполняя расчёты по формуле Мичелла, не замечали этого обстоятельства. Оно обнаружилось, когда Маскер свёл результаты расчётов волнового сопротивления для одной и той же модели Виглея, выполненные по линейной теории разными авторами, на один график. Он получил облако точек. Однако Маскер отнёс это не к особенностям интеграла Мичелла, а к особенностям линейной теории. Наша проверка, заключавшаяся в сравнении результатов аналитического интегрирования с численным интегрированием по методу Симпсона или трапеций, показала, что для получения необходимой точности результата требуется разбивать область интегрирования по длине судна не менее, чем на 1000 частей, а по осадке не менее, чем на 200, чего никто, конечно, никогда не делал. Интеграл (8), который имеет осциллирующую подынтегральную функцию, доставляет гораздо меньше хлопот, потому что для получения хорошего результата достаточно разбить отрезок интегрирования на 100 частей..
Второй важной проблемой, связанной с интегралом Мичелла, является наличие горбов и впадин на расчётных кривых там, где экспериментальные кривые имеют монотонный характер. Это не позволяет сравнивать разные формы обводов и, следовательно, применять формулу Мичелла для выбора формы корпуса при разработке теоретического чертежа реального судна. Горбы и впадины, которых нет на экспериментальных кривых, присущи не только кривой Мичелла, но и тем расчётным кривым волнового сопротивления, которые получают по нелинейным теориям. Сначала от них пытались избавиться с помощью поправочных коэффициентов, считая, что это происходит оттого, что в расчёте не учтено влияниепограничного слоя и попутного потока судна. Такое мнение сохраняется и по сей день. Для проверки этого обстоятельства нами был проведен эксперимент с двумя стойками, следующими друг за другом и создающими две автономные системы корабельных волн. Предполагалось, что при отсутствии между ними пограничного слоя на кривой волнового сопротивления этого тандема появятся горбы и впадины, как на кривой Мичелла, но экспериментальная кривая оказалась идентичной тем, которые получаются у моделей судов [12]. Таким образом, отпала гипотеза, в течение многих лет служившая объяснением различия между расчётными и экспериментальными кривыми волнового сопротивления. Эта загадка ждёт своего решения. До тех пор, пока не будет найдено объяснение этому явлению, все поиски новых и лучших теорий волнового сопротивления не приведут к успеху.
После преобразования интеграла Мичелла, которое позволило отделить монотонную (главную) часть от осциллирующей, нам удалось показать, что главная часть интеграла на малых относительных скоростях близко подходит к экспериментальным кривым волнового сопротивления и может служить критерием для сравнения разных форм обводов. Выбор формы оптимальных обводов по отношению главной части интеграла к водоизмещению показал хорошее совпадение с опытными данными. Осциллирующая часть интеграла Мичелла связана с интерференцией носовой и кормовой систем создаваемых судном волн [12].
Итак, следует отметить, что в настоящее время для практического использования проектанты не имеют ничего лучшего, чем главная часть интеграла Мичелла.
Особенность задачи о волновом сопротивлении судна заключается не только в горбах и впадинах на расчётных кривых, но и в том, что эта задача не поддаётся улучшению уже 100 лет после получения Мичеллем её решения в линейной постановке. На семинаре, проходившем в Токио в 1976 году, академик Руже Брар, затративший немало сил для решения проблемы вычисления сопротивления воды движению судна, говорил о том, что от конференции к конференции он надеялся на то, что решение будет, наконец, получено. Он повторил, что созданный в 1963 году в Анн Арборе комитет поставил цель разобраться в сущности сопротивления воды движению судов, обратив особое внимание на волновое сопротивление и соотношения между составляющими сопротивления, но «вот прошло 13 лет, и возникает мысль о том, что мы находимся в тупике».
Каждый, кто занимался задачей о волновом сопротивлении знает, что, несмотря на простоту постановки и кажущуюся возможность близкого решения, затраты времени и сил приводят только к появлению всё новых и новых проблем. Затративший всю свою творческую энергию на решение задачи о волновом сопротивлении бывший директор опытового бассейна им. Д.И. Менделеева замечательный учёный А.Н Смородин говорил, что в ХХ веке эта задача не может быть решена, потому что не будет достаточно мощных компьютеров. Но компьютеры уже есть, а проблем с этой задачей не уменьшается. Профессор А.М. Басин, выполнивший ряд фундаментальных работ в области гидромеханики корабля, завещал своему сыну М.А. Басину, одному из самых крупных специалистов в области гидромеханики судов, заниматься всем, кроме задачи о волновом сопротивлении. Гидромеханик Г.И. Зильман, затратив 10 лет на эту задачу и не получив никакого результата, вынужден был переключиться на другие проблемы ходкости, которые и продолжает успешно решать. К этому списку учёных можно добавить имена Дж. Вехаузена, К. Эггерса, Дж. Ньюмена, Ф. Ноблесса, М. Бесшо, Х. Маруо, Т. Инуи и десятки других известных имён учёных, упорно занимающихся этой проблемой.
Тех, кто подобно Мичеллу хочет дать проектировщикам формулу для расчёта волнового сопротивления, эта задача может привести в отчаяние и к мысли о бессилии науки. Какие процессы происходят при образовании волн вокруг движущегося судна в носу и в корме и дают основной вклад в волновое сопротивление? Сейчас ясно, что Ньютон и Эйлер были оба правы: есть и удар, и плавное обтекание. Нет только теории, учитывающей оба эти явления.
Работы Мичелла по свободным линиям тока и по волнам конечной высоты
Кроме работы по волновому сопротивлению, принесшей Мичеллу мировую славу, следует отметить ещё две его работы по гидромеханике. За несколько недель до своей смерти профессор А. Лав (A.E.H. Love, F.R.S) написал критические заметки о двух наиболее важных работах Мичелла [5a, 8a], куда включил обзор характера его работ в целом. Он писал: "те части работы Мичелла, которые я лучше знаю, были по теории свободных линий тока, а также была серия статей по различным разделам теории упругости, опубликованных в 1890 - 1902 годах”.
О работе Мичелла “On the theory of free stream lines” [5a] А.Лав писал: “Статьи по свободным линиям тока были первыми крупными статьями, опубликованными в нашей стране по теории разрывов в жидкости, которые возникают в струях и в попутном потоке. Разработка теории для двумерных течений жидкости была начата Гельмгольцем (1868), который получил решение задачи об истечении жидкости из большого сосуда через прямой канал. Это решение было впоследствии развито Кирхгоффом (1869 и 1883 годы) с помощью теории функций комплексного переменного. Кирхгофф предположил, что движение происходит в плоскости комплексной переменной z и определяется для любого частного случая путём нахождения функций w(z) таким образом, чтобы коэффициент при i в мнимой части w являлся функцией тока y. Вдоль свободных линий тока скорость и функция y постоянны. Кирхгофф заметил, что производная dz/dw которую он обозначил z, является комплексной переменной, модуль которой равен обратной величине скорости, а аргумент определяет направление этой скорости. Из этих наблюдений следовало, что задача с прямыми границами может быть решена эффективно с помощью конформных преобразований области z, ограниченной дугой окружности и отрезками радиальных линий, на плоскость w, ограниченную отрезками прямых”.
“В 80-х годах прошлого столетия несколько математиков, среди которых был Мичелл, работая независимо друг от друга, пришли к идее, что было бы перспективнее вместо функции Кирхгоффа z использовать её логарифм, обозначенный W , чтобы действительная часть W была постоянной величиной вдоль линии тока, а сопряжённая функция была постоянна вдоль прямолинейной границы. Мичелл это второе условие взял в такой форме, чтобы нормальная производная действительной части W равнялась нулю вдоль прямолинейной границы или вдоль эквивалентных ей отрезков параллельных прямых в w -плоскости. Известно, что преобразование Шварца-Кристоффеля конформно отображает область, ограниченную отрезками прямых, на полуплоскость, ограниченную бесконечной прямой. Мичелл применил это преобразование к области, ограниченной отрезками параллельных прямых y= const. в w -плоскости. Он конформно отобразил её на полуплоскость вспомогательной переменной u таким образом, чтобы отдельные отрезки бесконечной прямолинейной границы соответствовали линиям тока, а остальные части - прямым границам в плоскости z. Тогда W является функцией от u . Мичелл разработал условия, при которых функция W является потенциалом в u – полуплоскости, а при этом отрезки бесконечных граничных линий соответствуют линиям тока. Использование функции W, применение метода Шварца-Кристоффеля и трансформация задачи свободных линий тока в задачу электростатики являются оригинальными чертами исследований Мичелла. В этой же статье он применил полученную теорию к задаче электростатики о призматических проводниках, получил форму полых вихрей в двумерной области, ограниченной прямыми линиями. Полые вихри стали модными, благодаря исследованиям Хикса (W.M. Hicks). Конформные преобразования, как метод решения задач электростатики, были популяризованы в то время Томсоном (J.J.Thomson)”.
Профессор Т. Черри об этой же работе писал: «В статье "Free Stream Lines" (Свободные линии тока) [5а] Мичелл был первым, кто дал систематическую теорию предмета с применением преобразования Шварца-Кристоффеля. Предшествующая работа Кирхгоффа (Vorlesunger uber Mechanik; 1883), хотя подкреплялась частными примерами, явно требовала обобщения. Мичелл получил конформные преобразования в духе прикладной математики. Основываясь на электростатическом потенциале, он сформулировал задачу и потом написал очевидное решение. Среди примеров, которые он решил (в двумерной постановке, конечно), есть поток из прямоугольного судна через отверстие в днище, о струе через боковое отверстие трубы, о полых вихрях в жидкости между двумя параллельными плоскостями».
К этим мнениям коллег Мичелла следует добавить, что Мичелл сумел получить в общем виде формулу для конформного преобразования на вспомогательную плоскость u в таком виде, что при решении конкретной задачи оставалось определить только показатель степени nr. Мичелл показал на многочисленных примерах каким путём, исходя из условий задачи, можно получить этот показатель. При этом, он решил несколько задач об истечении жидкости через отверстия разной формы из сосудов и труб разного расположения, а также об истечении струи на плоскость, и те задачи, о которых упоминают А.Лав и Т. Черри.
О второй работе Мичелла по гидродинамике профессор Т. Черри писал: «В работе
"The highest waves in water" [8а] рассматривается безвихревое движение в двумерной
области с заострёнными гребнями волн. Используя отображение движения в плоскости
z = x +iy на плоскость потенциала скорости и функции тока w =
j + iy, Мичелл получил регулярную в полуплоскости
y > 0 и действительную на действительной оси функцию 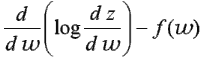 . Эта функция определена по всей
w – плоскости, где она имеет особенности только в виде полюсов в точках, соответствующих
гребням. Член f (w) был записан в виде рядов с неопределёнными коэффициентами, а
уравнение давления Бернулли было использовано для получения системы с бесконечным количеством условий. Начальные
члены рядов, таким образом, определяются, а сами ряды являются быстро сходящимися».
. Эта функция определена по всей
w – плоскости, где она имеет особенности только в виде полюсов в точках, соответствующих
гребням. Член f (w) был записан в виде рядов с неопределёнными коэффициентами, а
уравнение давления Бернулли было использовано для получения системы с бесконечным количеством условий. Начальные
члены рядов, таким образом, определяются, а сами ряды являются быстро сходящимися».
К высказыванию Т.Черри об этой работе следует добавить, что Мичелл был первым, кто определил с хорошейточностью профиль волн Стокса, а также нашёл предельное отношение высоты волны к её длине, равное 0,142.
Работы Мичелла по теории упругости
В связи с тем, что нам не приходилось заниматься задачами, связанными с теорией упругости, в этой части мы ограничиваемся тем, что написали профессора А. Лав и Т. Черри, а также тем, что из работ Мичелла помещено в монографии С.П. Тимошенко [13]. Профессор А. Лав (A.E.H. Love, F.R.S), внесший большой вклад в теорию упругости, был инициатором работ Мичелла в этой области. О работах Мичелла по теории упругости профессор А. Лав писал: «Во многих статьях, написанных Мичеллем по теории упругости, возможно, наиболее важной является одна, которая называется «On the direct determination of stress in an elastic solid with application to the theory of plates» (“Прямое определение напряжений в упругом теле и его применение к теории пластин”). Модные в то время методы определения напряжений были достаточно сложными (по выражению А. Лава, “окольными”). Развитая ранее теория показала, что напряжения в точке выражаются шестью составляющими, которые в настоящее время могут быть описаны симметричными тензорами второго порядка. Уравнения равновесия упругих тел являются тремя уравнениями в частных производных, которые связывают пространственные производные от составляющих напряжений с силами, которые действуют на тело (типа гравитационных). Эти уравнения иногда называют уравнениями равновесия напряжений. Упругие свойства тела выражается системой, связывающей составляющие напряжений с деформациями, в которой компоненты деформаций выражены как линейные функции пространственных производных от составляющих перемещений.
Выражая напряжения через деформации, а затем заменяя деформации перемещениями, уравнения равновесия напряжений трансформируются в систему дифференциальных уравнений в частных производных, связывающих перемещения с силами на теле. Эти уравнения, называемые иногда уравнениями перемещений, должны решаться так, чтобы были удовлетворены специальные условия перемещений или напряжения на границе тела. Определённые таким путём величины являлись перемещениями. Тогда деформации можно найти путём подстановки в уравнения, связывающие деформации с перемещениями, и напряжения можно вывести из деформаций с помощью соотношений напряжений -деформаций. В прямом методе это делается более результативно шаг за шагом. Эйри (G.B.Airy, 1862) заметил, что когда твёрдое тело, свободное от воздействия сил, находится в состоянии плоских напряжений, то три неисчезающие компоненты напряжений равны (с точностью до знаков) трём производным второго порядка одной функции, выраженной в декартовых координатах в плоскости системы напряжений. Эта функция впоследствии была названа функцией напряжений Эйри, и было показано, что она удовлетворяет определённым дифференциальным уравнениям в частных производных четвёртого порядка. Максвелл (1870) доказал, что для обыкновенного трёхмерного упругого свободного от воздействия сил тела могут потребоваться три таких функции напряжений, а Иббетсон (W.J. Ibbetson, 1887) нашёл, что эти функции должны удовлетворять системе уравнений в частных производных. Он это сделал путём подстановки соотношений напряжений-деформаций в систему из шести уравнений, которые были идентичны уравнениям Сен-Венана (Saint Venant, 1864) для составляющих деформаций».
«Мичелл (1900) отказался от ограничений, связанных с отсутствием сил, подставил вместо деформаций в уравнение Сен-Венана их выражения через составляющие напряжений и получил шесть независимых уравнений для компонент напряжений. Затем он упростил эти уравнения, скомбинировав их с уравнениями равновесия напряжений. В случае, когда на тело не действуют внешние силы, найденные Мичеллем уравнения, называемые иногда уравнениями совместности, приводятся к форме, разработанной Бельтрами (1892) в процессе рассмотрения альтернативной формы Морера для трёх функций напряжения Максвелла. Очевидно, Мичелл не знал об этой работе, так что, хотя его исследование было независимым, он вынужден разделить с Бельтрами первенство открытия. Зато он понял, что это даёт в первую очередь инструмент для ввода последовательности любых допущений, связанных с напряжениями. Он дал пример использования уравнений совместности напряжений для развития новой теории кручения и изгиба призм. Один из результатов Сен-Венана – это точное решение для случая изгиба безсдвига. Оно было применено Томсоном и Тайтом (Тait) к изгибу прямоугольной пластины парой, приложенной к её концам. Теория для пластин в состоянии плоских статических напряжений, когда плоскость напряжений параллельна невозмущённой стороне пластины, была разработана Клебшем (Clebsch). Мичелл заменил допущение о плоских напряжениях более общим распределением. Это дало возможность получить ряд точных решений, применимых к растяжению пластины в её плоскости при приложении пары сил к её концам, или для определения её деформаций под действием равномерных или равномерно изменяющихся давлений, приложенных к одной стороне поверхности. Чтобы получить решение для листа, который имеет границу в форме заданной кривой, необходимо найти плоские бигармонические функции для удовлетворения определённых условий на граничной кривой. Мичелл сделал это точно таким же способом, как это делается в теории призм Сен-Венана, когда необходимо определить плоские гармонические функции, чтобы удовлетворить условиям на кривой, ограничивающей поперечное сечения призмы. Таким образом, можно считать, что Мичелл сделал для плоской пластины то, что Сен-Венан сделал для призматического бруска».
Профессор Т.Черри о работах Мичелла по теории упругости писал: «Возможно, не меньше (чем работы по гидромеханике) известны работы Мичелла в области упругости [1а, 4а, 7а, 11а-22а]. В научном трактате А. Лава (A.E.H. Love) Мичелл представлен как один из тех, кто сделал главный вклад в литературу по этому предмету. Его работы относятся к периоду систематизации и обобщения теории, продолжавшей первые работы девятнадцатого столетия. Толчком для этого, несомненно, послужили публикации трактата A. Лава (1892 -1893), и результаты Мичелла могут быть видны при сравнении второй публикации А.Лава (1906) с первыми. Мичелл был первым, кто сформулировал полную систему уравнений упругости в зависимости только от составляющих напряжений. В этой же статье [11а] он показал, что такой путь приводит к особенно простому представлению двумерных систем уравнений упругости с помощью функции напряжений, и дал первое изложение теории для тонких пластин, свободное от сомнительных допущений. В следующей статье [12а] он проиллюстрировал эту теорию путём определения напряжений во вращающейся среде. Его открытие состояло в том, что, когда силы на теле отсутствуют, то функция напряжений в двумерном пространстве удовлетворяет бигармоническому уравнению. Это привело его к разработке обратного преобразования, использование которого в электростатике было показано на пятьдесят лет раньше Кельвином. Мичелл затем нашёл [22а], что из любого одного решения уравнения упругости в двух измерениях другое решение может быть получено с помощью инверсии. Он применил этот метод к решению интересных случаев напряжений в круговом цилиндре или диске, а также к решениям для тел с плоскими границами. В статьях по преобразованию напряжений [14а, 17а, 20а] он показал способ сведения задачи к определению гармонических функций по данным граничным условиям. Это была процедура, имеющая некоторое преимущество перед более специальным методом, применённым Бэтти (Betti)».
«Теория изгиба и кручения тонких стержней под действием силы или пары, приложенной только к концам, была подведена под общие принципы упругости Сен-Венаном и Клебшем в середине девятнадцатого столетия. Их метод был разработан при допущении, что напряжения поперёк любой плоскости, параллельной оси, отсутствуют, и они показали, что это отвечает физическим условиям. Мичелл заметил, что некоторые заключения могут быть получены из более общего предположения о том, что все составляющие напряжений линейны по координате z, и таким путём он нашёл ключ к теории стержней, равномерно нагруженных вдоль длины [21а]. Отсюда он смог определить ошибку в элементарной формуле Бернулли, связывающей изгибающий момент с кривизной».
Далее Т. Черри писал: “Его отношение к реальным приложениям теории упругости показано в многочисленных статьях [13а, 15а, 16а, 18а]. Например, в статье [18а] он рассмотрел балку сечения Ι, равномерно нагруженную вдоль верхней планки. Точное решение невозможно, но путём учёта того, что на практике главная функция хорд состоит не в несении нагрузки, а в обеспечении жёсткости стенки, он пришёл к значительным (и действительным) упрощениям задачи. Отсюда было получено её решение и сделано сравнение с инженерной практикой».
В книге С.П. Тимошенко [13] по теории упругости приводится много ссылок на работы Мичелла. Этих ссылок не меньше, чем на работы Сен-Венана и самого А. Лава. Если бы не те времена, когда в борьбе с космополитизмом исчезали из монографий и учебников имена иностранных учёных, то имя Мичелла упоминалось бы не только в связи с волновым сопротивлением, но и во всех наших учебниках по теории упругости.